Một vật có khối lượng m1 = 1,25 kg mắc vào lò xo nhẹ có độ cứng k = 200 N/m, đầu kia của lò xo gắn chặt vào tường. Vật và lò xo đặt trên mặt phẳng nằm ngang có ma sát không đáng kể. Đặt vật thứ hai có khối lượng m2 = 3,75 kg sát với vật thứ nhất rồi đẩy chậm cả hai vật cho lò xo nén lại 8 cm. Khi thả nhẹ chúng ra, lò xo đẩy hai vật chuyển động về một phía. Lấy pi^2=10m/s. khi lò xo giãn cực đại lần đầu tiên thì hai vật cách xa nhau một đoạn là:
A.(4pi-4)cm B.(2pi-4)cm C.16cm D.(4pi-8)cm
mọi người giúp mình suy luận nhanh với nhé :-)

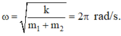
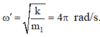




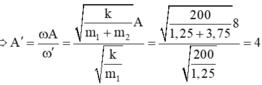

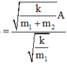
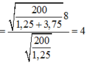
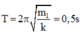




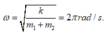
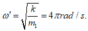

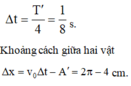
+ Giai đoạn 1: Hệ m1 + m2 cùng dao động từ biên ra vị trí cân bằng.
Tốc độ của hệ đạt đc khi đến VTCB là: \(v_{max}=\omega_{12}.A=\sqrt{\frac{200}{5}}.8=16\pi\)(cm/s)
+ Giai đoạn 2: Từ VTCB, hai vật tách nhau ra, m1 sẽ đi ra biên còn m2 vẫn giữ nguyên vận tốc vmax
Quãng đường m1 đi đc: \(A'=\frac{v_{max}}{\omega_1}=\frac{16\pi}{\sqrt{\frac{200}{1,25}}}=4cm\)
Quãng đường m2 đi đc: \(S=v_{max}.\frac{T_1}{4}=16\pi\frac{2\pi\sqrt{\frac{1,25}{200}}}{4}=2\pi\) cm.
Vậy khoảng cách 2 vật: \(2\pi-4\) cm.
Đáp án B.
Bài này còn có một cách suy luận nhanh là thế này: Ta biết dao động điều hòa là hình chiếu của 1 chuyển động tròn lên một trục tọa độ, mà vận tốc cực đại của dao động chính là tốc độ của chuyển động tròn đều.
Khi qua VTCB, vật m1, m2 cùng đạt tốc độ cực đại, trong khi m1 tiếp tục dao động điều hòa thì m2 lại chuyển động thẳng đều.
Như vậy, trong thời gian m1 đi từ VTCB ra biên thì m2 chuyển động trên cung tròn tương ứng ( bằng 1/4 vòng tròn).
+ Ta có biên độ dao động của m1 là 4cm.
+ Quãng đường m2 chuyển động là 1/4 chu vi của đường tròn tương ứng là: \(\frac{1}{4}.2\pi.R=\frac{1}{4}2\pi.4=2\pi\)cm
Từ đó suy ra khoảng cách 2 vật.