Một vật dao động điều hoà với chu kì T = 2s, trong 2s vật đi được quãng đường 40cm. Khi t = 0, vật đi qua vị trí cân bằng theo chiều dương. Phương trình dao động của vật làA.x = 10cos(2\(\pi\)t + \(\pi\)/2)(cm).B.x = 10sin(\(\pi\)t - \(\pi\)/2)(cm).C.x = 10cos(\(\pi\)t - \(\pi\)/2 )(cm).D.x = 20cos(\(\pi\)t +...
Đọc tiếp
Một vật dao động điều hoà với chu kì T = 2s, trong 2s vật đi được quãng đường 40cm. Khi t = 0, vật đi qua vị trí cân bằng theo chiều dương. Phương trình dao động của vật là
A.x = 10cos(2\(\pi\)t + \(\pi\)/2)(cm).
B.x = 10sin(\(\pi\)t - \(\pi\)/2)(cm).
C.x = 10cos(\(\pi\)t - \(\pi\)/2 )(cm).
D.x = 20cos(\(\pi\)t + \(\pi\))(cm).
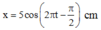
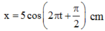
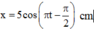
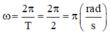
Phương trình tổng quát: \(x = Acos(\omega t +\varphi)\)
+ \(\omega = \frac{2\pi}{T} = \frac{2\pi}{2} = \pi\) (rad/s)
+ Nhận xét: Trong 2s = 1T, vật đi quãng đường 4.A = 40 cm, \(\Rightarrow\) A=10cm.
+ t = 0, vật qua VTCB theo chiều dương \(\Rightarrow\left\{ \begin{array}{} x_0 = 0\ cm\\ v_0 >0 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} \cos \varphi = 0\ \\ \sin \varphi <0 \end{array} \right. \Rightarrow \varphi = -\frac{\pi}{2}\)
Vậy phương trình: \(x = 10cos(\pi t -\frac{\pi}{2})\) (cm)