ta có: 
AH.BC = BK.AC 
10.BC = 12.AC 
=>BC= 6.AC/5 => BC^2=36.AC^2/25 
mặt khác: 
AC^2 = AH^2 + BC^2/4 = AH^2 + 36.AC^2/100 
=>(1-36/100). AC^2= AH^2 = 100 
=> AC^2 = 100^2/8^2 
=> AC = 100/8 = 25/2 
=> BC = 6.25/2.5=15

tam giac ACH đồng dạng tam giác BKC nên CA/AH = CB/BK 

Ai có thể giúp mình với!!!!!!!!!!!!!!!? | Yahoo Hỏi & Đáp

tự thế số vô

ta tính được AH=16(cm)

Suy ra Sabc=16²/2=128(cm²)

AH , BK cac duong cao 
ke HF vuong goc AC=>HF//=BE/2=6 
( tgBCE co HF duong trung binh) 
tgiac AHC vuong tai H , duong cao HF 
ta co 1/HF^2=1/AH^2+1/HC^2 
=>HC=HF*AH/can(AH^2-HE^2)=6.5 
=>BC=2HC=13 
2)ta co b^2=a.b' ; c^2=a.c' vay b'/c'=(b/c)^2 
do đó BD/CD=AB/AC(tinh chat duong pgiac) 
vay BH/CH=(BD/CD)^2=BD^2/CD^2 
ap dung tinh chat ty le thuc 
BH/(CH+BH)=BD^2/(BD^2+CD^2) 
BH/BC=BD^2/(BD^2+CD^2) 
vi BH+CH=BC=>thay so vao BH=6.3 
vay HD=BD-BH=1.2

 Kẻ AH vuông góc với BC, BK vuông góc với AC. 
Tam giác ABC cân tại A nên AB = AC. 
SABC = ½ AH . BC = ½ AH . 2BH (vì AH là đường cao của tam giác ABC cân tại A nên AH cũng là đường trung tuyến.→ BH = CH) 
SABC = ½ BK. AC 
Do đó: ½ AH. 2BH = ½ BK. AC 
→ AH . BH = ½ BK . AC 
→ 15,6 . BH = ½ . 12. AB (AB = AC) 
→ 15,6 . BH = 6. (AH + BH) 
→ 15,6 / 6 .BH = 15,6 + BH 
→ 2,6 BH = 15,6 + BH 
→ 2,6 BH – BH = 15,6 
→ 1,6 BH= 15,6 
→ BH = 15,6 : 1,6 
→ BH = 9,75 
→ BC = 2. 9, 75 = 19,5 

a/ vì (o) ngoại tiếp tam giác ABC => o là giao điểm 3 đường cao 

mà tam giác ABC cân tại A => đường cao AH đồng thời là trung trực của BC

=>O thuộc AH

lại có AH giao (o) tại D => AD là đường kính

bạn có thể cho mình xem hình không

Ta có: AH ⊥ BC ⇒ HB = HC = BC/2 = 24/2 = 12(cm)

Áp dụng định lí Pitago vào tam giác vuông ACH ta có:

A C 2 = A H 2 + H C 2

Suy ra: A H 2 = A C 2 - H C 2 = 20 2 - 12 2  = 400 - 144 = 256

AH = 16 (cm)

Tam giác ACD vuông tại C nên theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:

A C 2  = AH.AD ⇒ AD =  A C 2 /AH =  20 2 /16 = 25 (cm)

Vậy bán kính của đường tròn (O) là: R = AD/2 = 25/2 = 12,5 (cm)

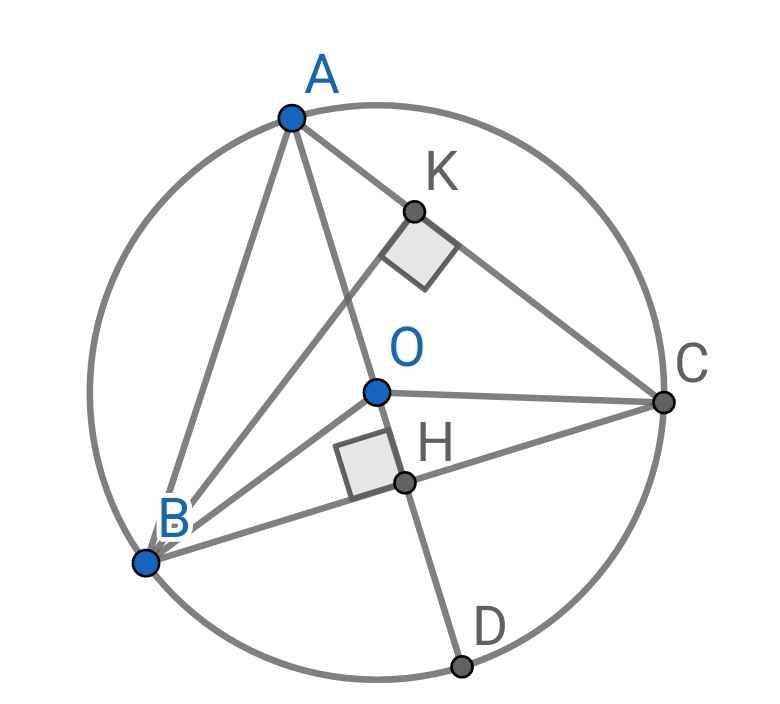 a) Ta có:

OB = OC (bán kính)

⇒ O nằm trên đường trung trực của BC (1)

Do ∆ABC cân tại A (gt)

AH là đường cao (gt)

⇒ AH cũng là đường trung trực của ∆ABC

⇒ AH là đường trung trực của BC (2)

Từ (1) và (2) suy ra O ∈ AH

⇒ O ∈ AD

Vậy AD là đường kính của (O)

b) Sửa đề: Tính độ dài các đường cao AH, BK của ∆ABC

Do AH là đường trung trực của BC (cmt)

⇒ H là trung điểm của BC

⇒ CH = BC : 2

= 12 : 2

= 6 (cm)

∆AHC vuông tại H

⇒ AC² = AH² + CH² (Pytago)

⇒ AH² = AC² - CH²

= 10² - 6²

= 64

⇒ AH = 8 (cm)

⇒ sinACH = AH/AC

= 4/5

⇒ ACH ≈ 53⁰

⇒ BCK ≈ 53⁰

∆BCK vuông tại K

⇒ sinBCK = BK/BC

⇒ BK = BC.sinBCK

= 10.sin53⁰

≈ 8 (cm)