A, DỄ DÀNG NHẬN THẤY AF VÀ BE LÀ CÁC TIA PHÂN GIÁC ( DO TAM GIÁC ABC ĐỀU)

=> CO LÀ TIA PHÂN GIÁC CỦA GÓC ACB

=> ACO = 30

DỄ DÀNG TÍNH ĐƯỢC OBC = 30

=> OBC = ACO

DO TAM GIÁC ABC ĐỀU => O LÀ GIAO ĐIỂM CỦA 3 ĐƯỜNG TRUNG TRỰC

=> OB = OC

TỪ ĐÓ DỄ DÀNG CHỨNG MINH ĐƯỢC TAM GIÁC OBM = TAM GIÁC OCN ( C.G.C)

=> OM = ON

B,  KẺ FH VUÔNG GÓC VỚI EF, NQ VUÔNG GÓC VỚI EF

DO CF = AE , CN = BM

=> MF = NE

LẠI CÓ GÓC NEQ = CEF = CFE = 60

=> NEQ = CFE

TỪ ĐÓ DỄ DÀNG CHỨNG MINH ĐƯỢC TAM GIÁC NQE = TAM GIÁC MHF ( G.C.G)

=> NQ = MH

TA CÓ NE SONG SONG VỚI MH , NQ = MH

=> MQNH LÀ HÌNH BÌNH HÀNH

=> QH CẮT MN TẠI TRUNG ĐIỂM CỦA MN

MÀ I LÀ TRUNG ĐIỂM CỦA MN

=> I THUỘC HQ

=> I THUỘC EF

=> ĐPCM

C, BÀI NÀY TỰ VẼ HÌNH NHÉ

TỪ M,N KỂ ĐƯỜNG VUÔNG GÓC VỚI AB CẮT AB TẠI H VÀ K. TỪ M KỂ ĐƯỜNG VUÔNG GÓC VỚI NK CẮT NK TẠI Q

=> MN LỚN HƠN HOẶC BẰNG MQ

MÀ MQ =HK

=> MN LỚN HƠN HOẶC BẰNG HK

MẶT KHÁC KA + HB = 1/2 AN + 1/2 BM = 1/2 AB = 1/2 BC = 1/2 AC

=> HK = 1/2 AB

=> MN LỚN HƠN HOẶC BẰNG 1/2AB

DẤU BẰNG XẢY RA KHI VÀ CHỈ KHI M VÀ N LÀ TRUNG ĐIỂM CỦA AC VÀ BC

( MÌNH MỚI HỌC LỚP 7)

Nhac cau 3

Tu M,N ke duong vuong goc voi AB cat AB tai H va K.Tu M ke duong vuong goc voi NK cat NK tai Q

=>MN\(_{\ge}\)MQ. Ma MQ=HK

=>MN\(\ge\)HK

Mat \(\ne\)KA+HB=1/2AN+1/2BM=1/2AB=1/2BC=1/2CA

=>HK=1/2AB

=>MN\(\ge\)1/2AB.dau bang xay ra khi M,N la trung diem cua cac canh

a) Ta có: ΔABC cân tại A(gt)

mà AM là đường trung tuyến ứng với cạnh đáy BC(M là trung điểm của BC)

nên AM là đường cao ứng với cạnh BC(Định lí tam giác cân)

⇒AM⊥BC(đpcm)

Ta có: M là trung điểm của BC(gt)

nên \(BM=MC=\dfrac{BC}{2}=\dfrac{6}{2}=3\left(cm\right)\)

Áp dụng định lí pytago vào ΔABM vuông tại M, ta được:

\(AB^2=AM^2+MB^2\)

\(\Leftrightarrow AM^2=AB^2-MB^2=5^2-3^2=16\)

hay AM=4(cm)

Vậy: AM=4cm

b) Ta có: AI+IB=AB(I nằm giữa A và B)

AJ+JC=AC(J nằm giữa A và C)

mà AB=AC(ΔABC cân tại A)

và AI=AJ(gt)

nên BI=CJ(đpcm)

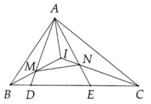
a) Tam giác ABE cân tại B có BI là phân giác nên cũng là đường cao, từ đó B I ⊥ A E . Tương tự  C I ⊥ A D .

b) Từ kết quả ý a, chứng minh được I là trực tâm tam giác AMN, từ đó  A I ⊥ M N

a: M đối xứng E qua AB

=>AB là đường trung trực của ME

=>AB\(\perp\)ME tại I và I là trung điểm của ME

Ta có: M đối xứng F qua AC

=>AC là đường trung trực của MF

=>AC\(\perp\)MF tại K và K là trung điểm của MF

Xét tứ giác AIMK có

\(\widehat{AIM}=\widehat{AKM}=\widehat{KAI}=90^0\)

=>AIMK là hình chữ nhật

b: Ta có: AKMI là hình chữ nhật

=>AK//MI và AK=MI; KM//AI và KM=AI

Ta có: MI//AK

I\(\in\)ME

Do đó: IE//AK

Ta có: AK=IM

IM=IE

Do đó: AK=IE

Ta có: AI=MK

MK=KF

Do đó: AI=KF

Ta có: AI//MK

K\(\in\)MF

Do đó: AI//KF

Xét tứ giác AKIE có

AK//IE

AK=IE

Do đó: AKIE là hình bình hành

=>KI//AE và KI=AE

Xét tứ giác AIKF có

AI//KF

AI=KF

Do đó: AIKF là hình bình hành

=>KI//AF và KI=AF

Ta có: KI//AF

KI//AE

AE,AF có điểm chung là A

Do đó: E,A,F thẳng hàng

Ta có: KI=AE

KI=AF

Do đó: AE=AF

mà E,A,F thẳng hàng

nên A là trung điểm của EF

Xét ΔABC có

M là trung điểm của AB

N là trung điểm của AC

Do đó: MN là đường trung bình của ΔABC

Suy ra: BC=2MN

hay BC=6(cm)