a. Chọn hệ quy chiếu Oxy như hình vẽ, chiều dương là chiều chuyển động. Vật chịu tác dụng của các lực f m s → ; N → ; P →

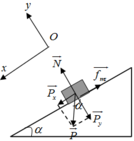
Theo định luật II newton ta có:  f → m s + N → + P → = m a → 1

Chiếu Ox ta có :

P x − f m s = m a 1 ⇒ P sin α − μ N = m a 1

Chiếu Oy ta có:  N = P y = P cos α

⇒ a 1 = g sin α − μ g cos α

⇒ a 1 = 10. 1 2 − 0 , 1.10. 3 2 = 4 , 134 m / s 2

Vận tốc của vật ở chân dốc.

Áp dụng công thức  v 1 2 − v 0 2 = 2 a 1 s

⇒ v 1 = 2 a 1 s = 2.4 , 134.40 ≈ 18 , 6 m / s

b. Chọn hệ quy chiếu Oxy như hình vẽ , chiều dương (+) Ox là chiều chuyển động .Áp dụng định luật II Newton

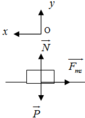
Ta có  F → m s + N → + P → = m a → 2

Chiếu lên trục Ox:  − F m s = m a 2 ⇒ − μ . N = m a 2 1

Chiếu lên trục Oy: N – P = 0 ⇒ N = P=mg

⇒ a 2 = − μ g = − 0 , 2.10 = − 2 m / s 2

Để vật dừng lại thì  v 2 = 0 m / s

Áp dụng công thức:

v 2 2 − v 1 2 = 2 a 2 . s 2 ⇒ s 2 = − 18 , 6 2 2. − 2 = 86 , 5 m

Chọn đáp án D

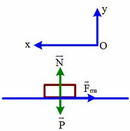
Chọn hệ quy chiếu Oxy như hình vẽ , chiều dương (+) Ox là chiều chuyển động

Áp dụng định luật II Newton

Ta có   

Chiếu lên trục Ox (1)

Chiếu lên trục Oy:  N-P=0 suy ra N=P=mg

Áp dụng công thức 

200g=0,2kg

các lực tác dụng lên vật khi ở trên mặt phẳng nghiêng

\(\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\)

chiếu lên trục Ox có phương song song với mặt phẳng nghiêng, chiều dương cùng chiều chuyển động

P.sin\(\alpha\)=m.a\(\Rightarrow\)a=5m/s²

vận tốc vật khi xuống tới chân dốc

v²-v₀²=2as\(\Rightarrow\)v=\(4\sqrt{5}\)m/s

khi xuống chân dốc trượt trên mặt phẳng ngang xuất hiện ma sát

các lực tác dụng lên vật lúc này

\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a'}\)

chiếu lên trục Ox có phương nằm ngang chiều dương cùng chiều chuyển động của vật

-F_ms=m.a'\(\Rightarrow-\mu.N=m.a'\) (1)

chiếu lên trục Oy có phương thẳng đứng chiều dương hướng lên trên

N=P=m.g (2)

từ (1),(2)\(\Rightarrow\)a'=-2m/s²

thời gian vật chuyển động trên mặt phẳng đến khi dừng lại là (v₁=0)

t=\(\dfrac{v_1-v}{a'}\)=\(2\sqrt{5}s\)

cái chỗ khi vật xuống dốc chiếu lên trục oX là P sin30-F ms mà

Oy :N-Pcos30

góc tạo bởi mặt phẳng nghiêng và phương ngang

sin\(\alpha=\dfrac{h}{l}\Rightarrow\alpha=30^0\)

\(\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\)

chiếu lên trục Ox phương song song mặt phẳng nghiêng, chiều dương cùng chiều chuyển động

sin\(\alpha\).P=m.a\(\Rightarrow\)a=5m/s²

thời gian vật đi hết dốc t=\(\sqrt{\dfrac{l}{2a}}\)=2s

b) khi đi hết dốc vận tốc của vật là v=v₀+a.t=10m/s²

khi xuống dốc xuất hiện ma sát

\(\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a'}\)

chiếu lên trục Ox phương nằm ngang chiều dương cùng chiều chuyển động

-F_ms=m.a' (1)

chiếu lên trục Oy phương thẳng đứng chiều dương hướng lên trên

N=P=m.g (2)

từ (1),(2)\(\Rightarrow\)a'=-5m/s²

thời gian vật chuyển động trên mặt phẳng đến khi dừng lại là (v₁=0)

t=\(\dfrac{v_1-v}{a'}=2s\)

Chọn đáp án A

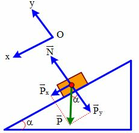
Chọn hệ quy chiếu Oxy như hình vẽ, chiều dương là chiều chuyển động. Vật chịu tác dụng của các lực 

Theo định luật II newton ta có:

Chiếu Ox ta có : 

Vận tốc của vật ở chân dốc.Áp dụng công thức

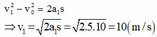
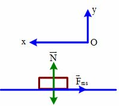
 Khi chuyển động trên mặt phẳng ngang

Chọn hệ quy chiếu Oxy như hình vẽ , chiều dương (+) Ox là chiều chuyển động .Áp dụng định luật II Newton

Ta có   

Chiếu lên trục Ox 

Để vật dừng lại thì 

Chiếu lên trục Oy 

Chọn hệ quy chiếu Oxy như hình vẽ, chiều dương là chiều chuyển động.

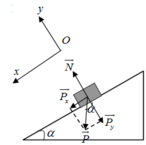
Vật chịu tác dụng của các lực  N → ; P →

Theo định luật II newton ta có:  N → + P → = m a → 1

Chiếu Ox ta có :  P x = m a 1 ⇒ P sin α = m a 1

⇒ a 1 = g sin α = 10. 5 10 = 5 m / s 2

Vận tốc của vật ở chân dốc.

Áp dụng công thức  v 1 2 − v 0 2 = 2 a 1 s

⇒ v 1 = 2 a 1 s = 2.5.10 = 10 m / s

Khi chuyển động trên mặt phẳng ngang: Chọn hệ quy chiếu Oxy như hình vẽ , chiều dương (+) Ox là chiều chuyển động .Áp dụng định luật II Newton

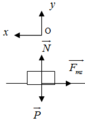
Ta có   F → m s + N → + P → = m a → 2

Chiếu lên trục Ox:  − F m s = m a 2 ⇒ − μ . N = m a 2 1

Chiếu lên trục Oy: N – P = 0 ⇒ N = P=mg

⇒ a 2 = − μ g = − 0 , 1.10 = − 1 m / s 2

Để vật dừng lại thì  v 2 = 0 m / s

Áp dụng công thức: 

v 2 2 − v 1 2 = 2 a 2 . s 2 ⇒ s 2 = − 10 2 2. − 1 = 50 m

Và  v 2 = v 1 + a 2 t ⇒ t = − 10 − 1 = 10 s

b) Khi vật chuyển động trên mặt ngang.

Chọn mốc thế năng tại chân mặt phẳng nghiêng.

a) Cơ năng tại đỉnh mặt phẳng nghiêng

\(W=mgh=mg.AB\sin 30^0=1,2.10.AB.\sin 30^0=24\)

\(\Rightarrow AB = 4(m)\)

b) Tại D động năng bằng 3 lần thế năng, ta có: \(W_đ=3W_t\Rightarrow W = 4W_t \Rightarrow W_t = 24: 4 = 6(J)\)

\(\Rightarrow mgh_1=mg.DB\sin 30^0=1,2.10.DB.\sin 30^0=6\)

\(\Rightarrow DB = 1(m)\)

c) Tại trung điểm mặt phẳng nghiêng

Thế năng: \(W_t = mgh_2=mg.\dfrac{AB}{2}\sin 30^0=1,2.10.2.\sin 30^0=12(J)\)

Động năng: \(W_đ=W-W_t=24-12=12(J)\)

\(\Rightarrow \dfrac{1}{2}.1,2.v^2=12\)

\(\Rightarrow 2\sqrt 5(m/s)\)

d) Công của lực ma sát trên mặt ngang: \(A_{ms}=\mu mg.S\)

Theo định lí động năng: \(W_{đ2}-W_{đ1}=-A_{ms}\Rightarrow 0-24=-\mu.1,2.10.1\Rightarrow \mu = 2\)

anh ơi , anh quên tính vận tốc của vật tại chân mặt phẳng nghiêng kìa . Đãng trí quá .