Các bạn giải giúp mình bài này với. Mình cảm ơn trước nha!
Tìm tập hợp điểm biểu diễn cho số phức z thỏa mãn: |iz-1|<=2 (bé hơn bằng 2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 9 2019
Đặt z = x + yi với x , y ∈ R . Suy ra z + z = 2x
z + z + i z + z = 2 z ⇔ 2 x + i 2 x = 2 x + 2 i y ⇔ 2 x = 2 x 2 x = 2 y ⇔ x ≥ 0 y = x
Vậy quỹ tích các điểm biểu diễn số phức z là tia phân giác của góc phần tư thứ nhất (bao gồm cả gốc tọa độ).
Đáp án B
CM
27 tháng 1 2017
Gọi số phức
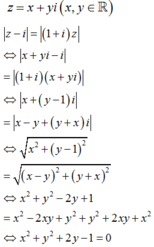
Vậy tập hợp biểu diễn số phức z thỏa mãn bài cho là đường tròn có phương trình x 2 + y 2 + 2 y - 1 = 0 có tâm I 0 , - 1 và bán kính R = 2
Chọn D.
CM
29 tháng 6 2018
Đáp án D
Đặt z = x + yi ta có
x + y i = 1 + i x + y i ⇔ x + y - 1 i = x - y x + y i
x 2 + y - 1 2 = x - y 2 + x + y 2 ⇔ x 2 + y 2 - 2 y - 1 = 0 ⇔ x 2 + y + 1 2 = 2
Vậy tập hợp các điểm biểu diễn các số phức z là đường tròn tâm bán kính R = 2
Giả sử : \(z=a+bi\left(a;b\in R\right)\) ; M(x;y) là điểm biểu diễn số phức z:
ta có: \(\left|\left(a+bi\right)i-1\right|\le2\) \(\Leftrightarrow\left|ai-b-1\right|\le2\) \(\Leftrightarrow a^2+\left(b+1\right)^2\le4\) \(\Leftrightarrow a^2+b^2+2b-3\le0\)
Vậy quỹ đạo của điểm M(z) là miền trong của hình tròn tâm I(0;-1) , bán kính R=2(Kể cả những điểm nằm trên đường tròn)