một máy phát điện xoay chiều 1 pha có roto là một nam châm điện có một cặp cực quay đều với tốc độ n(vòng/s)Một đoạn mạch RLC mắc nối tiếp vào hai cực của nhà máy. Khi roto quay với tốc độ n1 =60 (vòng/phút) thì dung khángcủa tụ điện bằng R; khi roto quay với tốc độ n2= 80 (vòng/phút) thì điện áp hiệu dụng ở hai đầu tụ điện maxBỏ qua điện trở thuần ở các cuộn dây phần ứng...
Đọc tiếp
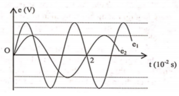
một máy phát điện xoay chiều 1 pha có roto là một nam châm điện có một cặp cực quay đều với tốc độ n(vòng/s)
Một đoạn mạch RLC mắc nối tiếp vào hai cực của nhà máy. Khi roto quay với tốc độ n1 =60 (vòng/phút) thì dung kháng
của tụ điện bằng R; khi roto quay với tốc độ n2= 80 (vòng/phút) thì điện áp hiệu dụng ở hai đầu tụ điện max
Bỏ qua điện trở thuần ở các cuộn dây phần ứng máy phát. Để cường độ dòng điện hiệu dụng qua mạch đạt giá trị cực
đại thì roto phải quay với tốc độ bằng
A. 240 vòng/phút B. 120 v/p C. 48 v/p D. 68 v/p
đáp án: B
thầy giúp em bài này với ạ.
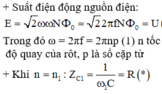
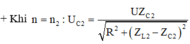
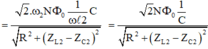
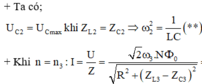
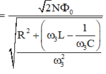
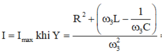
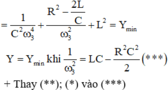
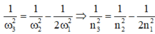
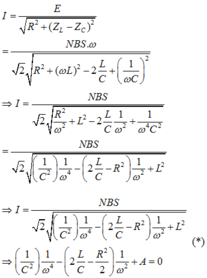
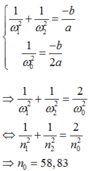
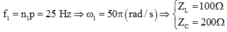
\(n=n_1=\dfrac{60v}{s} \Rightarrow R=Z_{C_1} \Rightarrow \omega _1.R.C=1 \)
\(n=n_2: U_C=\dfrac{\dfrac{\Phi}{\sqrt2}.\omega .\dfrac{1}{\omega .C}}{\sqrt{\left(Z_L-Z_C\right)^2+R^2}}=\dfrac{\dfrac{\Phi}{\sqrt2}.\dfrac{1}{C} }{\sqrt{\left(Z_L-Z_C\right)^2+R^2}} \)
\(U_{C_{max}} \Leftrightarrow Z_L=Z_C\rightarrow LC=\dfrac{1}{\omega _2^2} \)
\(I=\dfrac{\dfrac{\Phi}{\sqrt2}.\omega }{\sqrt{\left(Z_L-Z_C\right)^2+R^2}} \)
\(n=n_3 \) Thay đổi \(\omega \) để I max trong trường hợp này tương tự thay đổi \(\omega\) để \(U_L\) max trong mạch RCL nối tiếp
\(\rightarrow \dfrac{1}{\omega _3.C} =\sqrt{\dfrac{L}{C}-\dfrac{R^2}{2}} \rightarrow \omega _3=\dfrac{1}{C.\sqrt{\dfrac{L}{C}-\dfrac{R^2}{2} }}=\dfrac{1}{\sqrt{LC-\dfrac{R^2C^2}{2}}}\)
\(=\dfrac{1}{\sqrt{\dfrac{1}{\omega _2^2}-\dfrac{\left(\dfrac{1}{\omega _1^2}\right) }{2} } } \)
Vậy:\(n_3=\dfrac{1}{\sqrt{\dfrac{1}{n_2^2}-\dfrac{1}{2.n_1^2} }}=240 \dfrac{v}{s}\)
ad cho em hỏi sao Uc max lại là cộng hưởng U I max giống UL max em tưởng UC max với UL max có Ct tính gần giống nhau chứ