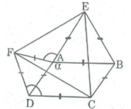
Ta có:

∠ (BAD) + ∠ ∠ (ADC) = 180 0  (hai góc trong cùng phía bù nhau)

⇒  ∠ (ADC) =  180 0  -  ∠ (BAD) =  180 0  – α

∠ (CDF) =  ∠ (ADC) +  ∠ (ADF) =  180 0  - α 2 + 60 0 = 240 0 - α

Suy ra:  ∠ (CDF) =  ∠ (EAF)

Xét  ∆ AEF và ∆ DCF: AF = DF ( vì  ∆ ADF đều)

AE = DC (vì cùng bằng AB)

∠ (CDF) =  ∠ (EAF) (chứng minh trên)

Do đó:  ∆ AEF =  ∆ DCF (c.g.c) ⇒ EF = CF (1)

∠ (CBE) =  ∠ (ABC) + 60 0 = 180 0 - α + 60 0 = 240 0 - α

Xét ΔBCE và ΔDFC: BE = CD ( vì cùng bằng AB)

∠ (CBE) =  ∠ (CDF) = 240 0 - α

BC = DF (vì cùng bằng AD)

Do đó  ∆ BCE =  ∆ DFC (c.g.c) ⇒ CE = CF (2)

Từ (1) và (2) suy ra: EF = CF = CE

Vậy  ∆  ECF đều.

Xét ΔAEF và ΔDCF có

AE=DC

góc EAF=góc CDF

AF=DF

=>ΔAEF=ΔDCF

=>FE=CF

Xét ΔDCF và ΔBEC có

DC=BE

góc CDF=góc EBC

DF=BC

=>ΔDCF=ΔBEC

=>CF=CE

=>CF=CE=FE

=>ΔCEF đều

Em tự vẽ hình nhé. Như sau:

Dễ thấy \(\widehat{AEB}=\widehat{CEF}=60^o\)nên \(\widehat{BEC}=\widehat{AEF}\)

Lại có \(\Delta AEB\)đều nên EA=EB. \(\Delta CEF\)đều nên EC=EF

Do đó \(\Delta EBC=\Delta EAF\left(c-g-c\right)\)=> BC=AF

\(\Delta ADF\)đều nên AF=AD

=> BC=AD (=AF)

Cmtt:CD=AB

Vậy ABCD là hbh

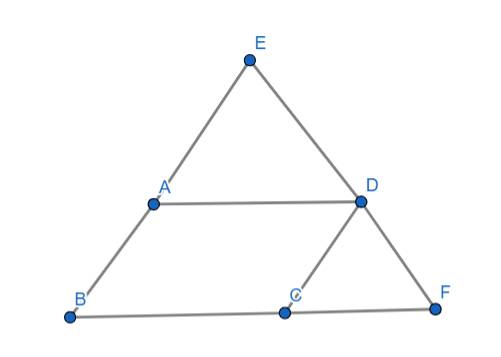
Đặt độ dài cạnh AD là a, độ dài cạnh AB là b

Ta có: ABCD là hình bình hành nên:

\(AB=CD=b\) (hai cạnh bên) 

Mà: DCF là tam giác đều nên: 

\(CD=CF=DF=b\) (ba cạnh tam giác đều) 

Và: \(AD=BC=a\)

\(\Rightarrow BF=BC+CF=a+b\) (1)

Và: ΔADE là tam giác đều nên:

\(AD=DE=AE=a\) 

\(\Rightarrow BE=AB+AE=a+b\) (2) 

\(\Rightarrow EF=DE+DF=a+b\) (3) 

Từ (1) và (2) và (3)

\(\Rightarrow BE=BF=EF=a+b\)

Vậy ΔBEF là tam giác đều (đpcm) 

BE EF BF k p đường thẳng b oi

Hình bình hành lớp 8? | Yahoo Hỏi & Đáp

Tính góc EAF 

EAF^ = 360* - (DAF^ + BAD^ + BAE^) = 360* - (60* + a + 60*) = 240* - a (1) 

b) Chứng minh rằng tam giác CEF là tam giác đều 

ABC^ = ADC^ = 180* - a 

=> CDF^ = ADC^ + ADF^ = 180* - a + 60* = 240* - a (2) 

CBE^ = ABC^ + ABE^ = 180* - a + 60* = 240* - a (3) 

AF = DF = AD = BC (4) 

CD = AB = BE = AE (5) 

(1) (2) (3) (4) và (5) => Δ CDF = ΔEBC = Δ EAF ( c.g.c) 

=> CF = CE = EF => CEF là tam giác đều

Xét tam giác ABD và tam giác FBC có:

AB=FB ( cạnh tam giác đều FAB)

DB=BC ( cạnh tam giác đều DBC)

góc ABD = góc FBC ( cùng bằng góc ABC + 60 độ)

Suy ra tam giác ABD = tam giác FBC (C.G.C)

=> FC=AD

Giả sử tứ giác ABCD định hướng âm. Gọi \(f\) là phép quay vec tơ theo góc \(\frac{\pi}{3}\) ta có

\(\overrightarrow{EG}=\overrightarrow{AG}-\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{BG}-\overrightarrow{AE}\)

suy ra \(f\left(\overrightarrow{EG}\right)=f\left(\overrightarrow{AB}\right)+f\left(\overrightarrow{BG}\right)-f\left(\overrightarrow{AE}\right)\)

                        \(=\overrightarrow{AE}+\overrightarrow{BC}-\overrightarrow{BE}\)

                        \(=\overrightarrow{AC}\)

Tương tự ta cũng chứng minh được \(f\left(\overrightarrow{HF}\right)=\overrightarrow{AC}\)

Từ đó suy ra \(\overrightarrow{EG}=\overrightarrow{HF}\)

Do đó tứ giác EGFH là hình bình hành