Tìm m để y = 2x3-3(2m+1)x2+6m(m+1)x+2 có 2 điểm cực trị trái dấu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+ Ta có: y’ = 6x2-6( 2m+1) x+ 6m(m+1)
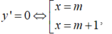
do đó hàm số luôn có cực đại cực tiểu với mọi m.
+ Tọa độ các điểm CĐ, CT của đồ thị là A( m; 2m3+3m2+1 ) và B( m+1; 2m3+3m2)
Suy ra AB = √2 và phương trình đường thẳng AB: x+ y-2m3-3m2-m-1=0.
+ Do đó, tam giác MAB có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ M tới AB nhỏ nhất.
d ( M , A B ) = 3 m 2 + 1 2 ⇒ d ( M , A B ) ≥ 1 2 ⇒ m i n d ( M , A B ) = 1 2
đạt được khi m=0
Chọn B

Chọn B
Ta có:
![]()
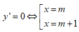
⇒ ∀ m ∈ ℝ , hàm số luôn có CĐ, CT
Tọa độ các điểm CĐ, CT của đồ thị là
![]()
Suy ra A B = 2
và phương trình đường thẳng x + y - 2 m 3 - 3 m 2 - m - 1 = 0
Do đó, tam giác MAB có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ M tới AB nhỏ nhất.
Ta có:
![]()
![]()
⇒ đạt được khi m = 0

a) y′ = 3 x 2 + 2(m + 3)x + m
y′ = 0 ⇔ 3 x 2 + 2(m + 3)x + m = 0
Hàm số đạt cực trị tại x = 1 thì:
y′(1) = 3 + 2(m + 3) + m = 3m + 9 = 0 ⇔ m = −3
Khi đó,
y′ = 3 x 2 – 3;
y′′ = 6x;
y′′(1) = 6 > 0;
Suy ra hàm số đạt cực tiểu tại x = 1 khi m = 3.
b) y′ = −( m 2 + 6m) x 2 − 4mx + 3
y′(−1) = − m 2 − 6m + 4m + 3 = (− m 2 − 2m – 1) + 4 = −(m + 1)2 + 4
Hàm số đạt cực trị tại x = -1 thì :
y′(−1) = − ( m + 1 ) 2 + 4 = 0 ⇔ ( m + 1 ) 2 = 4
⇔ 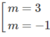
Với m = -3 ta có y’ = 9 x 2 + 12x + 3
⇒ y′′ = 18x + 12
⇒ y′′(−1) = −18 + 12 = −6 < 0
Suy ra hàm số đạt cực đại tại x = -1.
Với m = 1 ta có:
y′ = −7 x 2 − 4x + 3
⇒ y′′ = −14x − 4
⇒ y′′(−1) = 10 > 0
Suy ra hàm số đạt cực tiểu tại x = -1
Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.

Chọn B
Phương pháp:
Tính y'.
Tìm m để ![]()
Cách giải:
Ta có ![]()
![]()
Xét phương trình y' = 0 ![]() có
có ![]()
Suy ra phương trình y' = 0 luôn có hai nghiệm ![]()
Dễ thấy ![]() trong khoảng
trong khoảng ![]() thì hàm số đồng biến.
thì hàm số đồng biến.
Bài toán thỏa ![]()
Do ![]()
![]()
Vậy có ![]() giá trị của m thỏa mãn bài toán.
giá trị của m thỏa mãn bài toán.
Chú ý:
Cách khác: Tìm m để ![]()
Theo định lí Viet, ta có 
Hàm số đồng biến trên
(
2
;
+
∞
)
⇔
phương trình y' = 0 có hai nghiệm ![]()
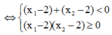
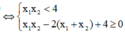

![]()
![]()
Vậy có 1001 số nguyên m thuộc khoảng (-10000;10000)

Ta có
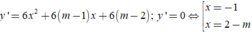
Để hàm số có hai cực trị kh y’=0 có hai nghiệm phân biệt
⇔ 2 - m ≠ - 1 ⇔ m ≠ 3
● Nếu -1<2-m hay m<3,
ycbt 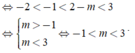
● Nếu 2-m<-1 hay m>3, ycbt
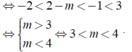
Vậy m ∈ - 1 ; 3 ∪ 3 ; 4
Chọn A.
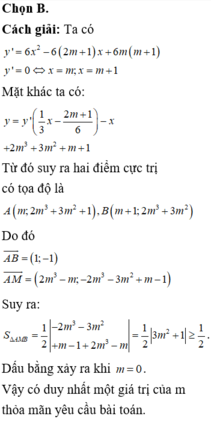

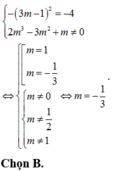

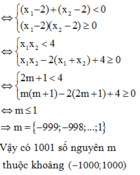
ta co y'=6x2-6(2m+1)x+6m(m+1). de co 2 diem cuc tri trai dau thi y'=0 co 2no fb <=>Δ'>0 P<O theo vi-et: x1.x2=m(m+1) <=>Δ'=9>0(dung) m(m+1)<0<=>-1<m<0