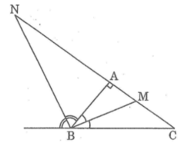
cho tam giác ABC vuông tại A có AB=6cm,AC=8cm. Các đường phân giác trong và ngoài của góc B cắt AC lầ lượt tại E và D. Tính đoạn thẳng BD,BE.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì BM là đường phân giác của góc B nên ta có:
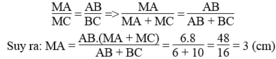
Vì BN là đường phân giác của góc ngoài đỉnh B nên ta có: BM ⊥ BN
Suy ra tam giác BMN vuông tại B
Theo hệ thức liên hệ giữa đường cao và hình chiếu hai cạnh góc vuông, ta có: A B 2 = AM.AN
Suy ra: AN = ![]() = 12 (cm)
= 12 (cm)


Áp dụng định lý Pitago cho ABH vuông tại A có:
![]()
![]()
Vì BM là tia phân giác trong của góc B ⇒ M A M C = A B B C (Tính chất đường phân giác)
⇒ M A M C + M A = A B B C + A B ⇒ M A A C = A B B C + A B ⇒ M A 8 = 6 10 + 6 ⇒ MA = 3cm
Vì BM; BN là tia phân giác trong và ngoài của góc B ⇒ N B M ^ = 90 0
Áp dụng hệ thức lượng trong ABM vuông tại B có đường cao BA ta có:
![]()
Đáp án cần chọn là: D

a/ Xét tg HBA và tg ABC, có:
góc BHA = góc BAC = 90 độ
góc B chung
Suyra: tg HBA đồng dạng với tg ABC (g-g)
b/ Ta có tg ABC vuông tại A:
\(BC^2=AC^2+AB^2\)
\(BC^2=8^2+6^2=100\)
\(\Rightarrow BC=\sqrt{100}=10\)(cm)
Ta có: \(\frac{HA}{AC}=\frac{BA}{BC}\)(tg HBA đồng dạng với tg ABC)
\(\Rightarrow\frac{HA}{8}=\frac{6}{10}\)
\(\Rightarrow HA=\frac{8.6}{10}=4,8\left(cm\right)\)

Cách 1:
\(AC=\sqrt{BC^2-AB^2}=8\) cm
Từ D kẻ \(DH\perp BC\) tại H
Xét hai tam giác vuông DHB và DAB có:
\(\widehat{DBH}=\widehat{DBA}\) ( do BD là tia phân giác góc B)
BD chung
Nên \(\Delta DHB=\Delta DAB\left(ch-gn\right)\)
Suy ra \(HB=AB=6cm\Rightarrow HC=4cm\) và \(DH=DA\)
Áp dụng định lý pytago vào tam giác DHC vuông tại H có:
\(DC^2=4^2+DH^2\) \(\Leftrightarrow\left(AC-AD\right)^2=16+DA^2\)
\(\Leftrightarrow\left(8-AD\right)^2=16+AD^2\)
\(\Leftrightarrow AD=3\) \(\Rightarrow BD=\sqrt{AD^2+AB^2}=3\sqrt{5}\) cm
Cách 2:
\(\dfrac{DC}{DA}=\dfrac{BC}{BA}=\dfrac{10}{6}=\dfrac{5}{3}\)\(\Leftrightarrow\dfrac{DC}{5}=\dfrac{DA}{3}=\dfrac{DC+DA}{5+3}=\dfrac{AC}{8}=\dfrac{8}{8}=1\)
\(\Rightarrow DC=5,DA=3\)
Làm tương tự như trên
o. Tính BE
Có \(\dfrac{EA}{EC}=\dfrac{BA}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
\(\Leftrightarrow\dfrac{EA}{EA+AC}=\dfrac{3}{5}\Leftrightarrow\dfrac{EA}{EA+8}=\dfrac{3}{5}\Leftrightarrow EA=12\)
\(BE=\sqrt{ED^2-BD^2}=\sqrt{\left(EA+AD\right)^2-BD^2}=6\sqrt{5}\) ( \(BE\perp BD\) do hai đường phân giác của hai góc kề bù)
Kết luận:...