một vật bắt đầu chuyển động nhanh dần đều từ trạng thái đứng yên và đi được quãng đường s trong 6s. Tìm thời gian mà vật đi được trong 3/4 sau của đoạn đường s.
MÌNH KHÔNG HIỂU CÂU NÀY, NHỜ CÁC BẠN GIÚP MÌNH.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 11 2021
Gọi t là thời gian đi cả quãng đường.
\(t_1\) là thời gian đi \(\dfrac{1}{4}\) đoạn đường đầu.
Ta có: \(S=\dfrac{1}{2}at^2\)
\(\dfrac{1}{4}S=\dfrac{1}{2}at^2_1\)
\(\Rightarrow\dfrac{S}{\dfrac{1}{4}S}=\dfrac{\dfrac{1}{2}at^2}{\dfrac{1}{2}at^2_1}=\dfrac{t^2}{t^2_1}\)\(\Rightarrow t_1=\dfrac{t}{2}\)
Thời gian vật đi \(\dfrac{3}{4}\) đoạn đường cuối:
\(t'=t-t_1=t-\dfrac{t}{2}=\dfrac{t}{2}\left(h\right)\)
VT
25 tháng 3 2017
+ Gọi t là thời gian vật đi hết quãng đường S nên t=4s, thời gian để vật đi hết 3 4 quãng đường cuối là n
VT
14 tháng 2 2019
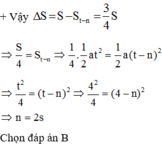
Giải: Ta có v 0 = 0 ( m / s )
Gọi t là thời gian vật đi hết quãng đường S nên t=4s, thời gian để vật đi hết 3 4 quãng đường cuối là n
Vậy Δ S = S − S t − n = 3 4 S ⇒ S 4 = S t − n ⇒ 1 4 . 1 2 a t 2 = 1 2 a ( t − n ) 2 ⇒ t 2 4 = ( t − n ) 2 ⇒ 4 2 4 = ( 4 − n ) 2 ⇒ n = 2 s
Chọn gốc tọa độ tại nơi vật bắt đầu xuất phát, mốc thời gian từ lúc vật bắt đầu chuyển động, chiều dương là chiều chuyển động.
(Thời gian đi 3/4 quãng đường cuối = thời gian đi cả quãng đường - thời gian đi 1/4 quãng đường đầu)
Ta có:
- Cả quãng đường đi với thời gian là t (giây):
\(s=v_0t+\frac{1}{2}at^2=\frac{1}{2}at^2\) (*)
\(\frac{1}{4}s=v_0t'+\frac{1}{2}a\left(t'\right)^2=\frac{1}{2}a\left(t'\right)^2\) (**)
(Vì v(0) = 0)
Lấy (*) chia (**) \(\frac{t^2}{\left(t'\right)^2}=4\Rightarrow t'=\frac{1}{2}t\)
Thời gian đi 3/4 quãng đường cuối là:
\(t''=t-t'=t-\frac{1}{2}t=\frac{1}{2}t\)
+ Thời gian đi đoạn đường S là 6s.
+ Tìm thời gian đi 1/4 đoạn đường S ban đầu là t1
+ Từ đó suy ra thời gian đi 3/4 đoạn đường sau là: t2 = 6 - t1