Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
dựa vào định nghĩa giao tuyến : là tập hợp các điểm chung của 2 mặt phẳng ( 2 mặt phẳng cắt nhau ).
giả sử M là giao điểm a, b , M ko thuộc delta ta có :
M thuộc mặt phẳng (P) ( do M thuộc a )
M thuộc mặt phẳng (Q) ( do M thuộc b)
suy ra M là điểm chung 2 mặt phẳng .
theo định nghĩa trên, M phải thuộc giao tuyến. vậy điểu giả sử là sai .
Kết luận : M thuộc giao tuyến.
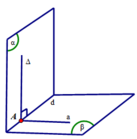
Δ nằm trong (α) và Δ vuông góc với d ⇒ Δ cắt d tại A
Từ A, vẽ đường thẳng a thuộc (β) và a ⊥ d
Khi đó góc giữa 2 mp (α) và (β) bằng góc giữa hai đường thẳng ∆ và a.
Vì (α) ⊥ (β) nên góc giữa Δ và a là 90° hay Δ ⊥ a
⇒ Δ ⊥ (d,a) hay Δ ⊥ (β)
a) Sai
Sửa lại: "Đường thẳng Δ là đường thẳng vuông góc chung của hai đường thẳng chéo nhau a và b nếu Δ cắt cả a và b, đồng thời Δ ⊥ a và Δ ⊥ b"
b) Đúng
c) Đúng
d) Sai
Sửa lại: Đường thẳng đi qua M trên a và vuông góc với a, đồng thời cắt b tại N và vuông góc với b thì đó là đường vuông góc chung của a và b.
e) Sai.
*Tìm giao tuyến của 2 mặt phẳng (M,a) và (M,b):
Có M là một điểm chung
Theo bài : a và b cắt nhau tại O
=> O thuộc a ⊂ (M,a) =>O thuộc (M,a)
và O thuộc b ⊂ (M,b) =>O thuộc (M,b)
=>O là điểm chung thứ hai
Vậy: (M,a) ∩ (M,b) = OM
Do đó giao tuyến OM lun thuộc mặt phẳng tạo bởi c và O ( mp (O,c)) là một mp cố định.
