Cho n đường thẳng phân biệt d1 ; d2 ; d3; ... ; dn đôi một cắt nhau và không có ba đường nào đồng qui . Hỏi có bao nhiêu giao điểm tạo thành ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 3 2017
Chọn C
* Số tam giác có 2 đỉnh thuộc
d
1
và 1 đỉnh thuộc
d
2
là: 
.
* Số tam giác có 1 đỉnh thuộc
d
1
và 2 đỉnh thuộc
d
2
là: 
.
Vậy có 70 + 105 = 175 tam giác.
CM
14 tháng 12 2017
Tam giác cần lập thuộc hai loại
Loại 1: Tam giác có một đỉnh thuộc d1 và hai đỉnh thuộc d2. Loại này có 
tam giác.
Loại 2: Tam giác có một đỉnh thuộc d2 và hai đỉnh thuộc d1. Loại này có 
tam giác.
Theo bài ra ta có: 
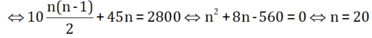
Chọn A.
CM
7 tháng 5 2017
Tam giác cần lập thuộc hai loại
Loại 1: Tam giác có một đỉnh thuộc d 1 và hai đỉnh thuộc d 2 .
Loại này có C 10 1 . C n 2 tam giác.
Loại 2: Tam giác có một đỉnh thuộc d 2 và hai đỉnh thuộc d 1 .
Loại này có C 10 2 . C n 1 tam giác.
Theo bài ra ta có: C 10 1 . C n 2 + C 10 2 . C n 1 = 2800
⇔ 10 n ( n − 1 ) 2 + 45 n = 2800 ⇔ n 2 + 8 n − 560 = 0 ⇔ n = 20
Chọn đáp án D
CM
13 tháng 1 2019
Có 2 trường hợp sau:
+ Lấy 1 điểm trên d1 và 2 điểm trên d2, suy ra cớ 10 C n 2 tam giác
+ Lấy 2 điểm trên d1 và 1 điểm trên d2, suy ra cớ n C 10 2 tam giác
Suy ra có
CM
30 tháng 9 2019
Đáp án B
Có 2 trường hợp sau:
+ Lấy 1 điểm trên d1 và 2 điểm trên d2, suy ra cớ 10 C n 2 tam giác
+ Lấy 2 điểm trên d1 và 1 điểm trên d2, suy ra cớ n C 10 2 tam giác
Suy ra có
CM
31 tháng 5 2018
Chọn đáp án D
Một điểm bất kì trên đường thẳng d1 với hai điểm phân biệt trên d2 hoặc cứ một điểm bất kì trên đường thẳng d2 với hai điểm phân biệt trên d1 tạo thành một tam giác.
Vậy tổng sổ tam giác thỏa mãn đề bài là 
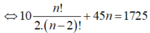
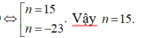
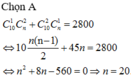
Có tất cả n đường thẳng phân biệt. Cứ mỗi đường thẳng thì có thể kết hợp với (n-1) đường thẳng còn lại để tạo ra (n-1) giao điểm.
Suy ra số giao điểm là : \(\frac{n\left(n-1\right)}{2}\) (Vì số lần lặp lại hai đường thẳng giao nhau là 2)
tạm