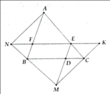
Cho tam giác ABC có AB=AC và điểm K bất kì nằm giữa hai điểm A và B . Từ K vẽ đường
thẳng song song AC cắt BC tại E . Gọi M là trung điểm của EC .
a) Chứng minh KB=KE
b) Đường thẳng KM cắt đường thẳng AC tại N . Chứng minh: KC//EN và KB=NC .
c) Chứng minh AK+AN không đổi khi K thay đổi.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
\(\widehat{KEB}=\widehat{C}\)(hai góc đồng vị, KE//AC)
Do đó: \(\widehat{KBE}=\widehat{KEB}\)
Suy ra: ΔKEB cân tại K
hay KB=KE

a: HM là đường trung bình của ΔEBC
=>EH=HB
KM là đường trug bình của ΔFBC
=>FK=KC
ΔAHM có EO//HM
=>AE/AH=AO/AM
ΔAKM có KM//FO
nên AF/AK=AO/AM
=>AE/AH=AF/AK
=>EF//HK
b: ΔAHM có EO//HM
=>MA/MO=HA/HE
=>MA/MO=HA/HB
ΔAKM có FO//KM
=>MA/MO=KA/KF=KA/KC
=>HA/HB=KA/KC
=>HK//BC
=>EF//BC

a,xet tam giac AKB va tam giac AKC co:
BK=CK(gt)
AK canh chung
AB=AC(gt)
=>tam giac AKB=tam giac AKC(c.c.c)
b,xet tam giacABC co:
AB=AC=>tam giac ABC can tai A
=>AK vua la duong trung truc, vua la duong cao
=>AK vuong goc voi BC
c,ta co: AK vuong goc voi BC, CE vuong goc voi BC
=>CK song song voi CE

Cho tam giác ABC vuông tại A có AB AC = . Gọi K là trung điểm của BC. 1) Chứng minh = AKB AKC . 2) Qua C vẽ đường thẳng vuông góc với BC cắt AB tại E . Tính số đo góc AEC.