Bài 1: Cho tam giác ABC vuông tại A. Vẽ I,K lần lượt là trung điểm của AB,BC. Gọi D là điểm đối xứng của A qua K.a. Chứng minh tứ giác ABDC là hình chữ nhật.b. Gọi E là điểm đối xứng của K qua I. Chứng minh tứ giác AKBE là hình thoi.c. Chứng minh tứ giác AEKC là hình bình hành.d. Tìm điều kiện để hình thoi AKBE là hình vuông.Bài 2: Cho tam gaics ABC vuông tại A, đường cao AH, trung tuyến AM. Gọi D...
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A. Vẽ I,K lần lượt là trung điểm của AB,BC. Gọi D là điểm đối xứng của A qua K.
a. Chứng minh tứ giác ABDC là hình chữ nhật.
b. Gọi E là điểm đối xứng của K qua I. Chứng minh tứ giác AKBE là hình thoi.
c. Chứng minh tứ giác AEKC là hình bình hành.
d. Tìm điều kiện để hình thoi AKBE là hình vuông.
Bài 2: Cho tam gaics ABC vuông tại A, đường cao AH, trung tuyến AM. Gọi D là trung điểm AB, lấy điểm E đối xứng với M qua D.
a. Chứng minh: M và E đối xứng nhau qua AB.
b. Chứng minh: AMBE là hình thoi.
c. Kẻ HK vuông góc với AB tại K, HI vuông góc với AC tại I. Chứng minh IK vuông góc với AM
Bài 3: Cho tam giác ABC có ba góc nhọn, trực tâm H. Đường thẳng vuông góc với AB kẻ từ B cắt từ đường thẳng vuông góc từ AC kẻ từ C tại D.
a. Chứng minh tứ giác BHCD là hình bình hành.
b. Gọi M là trung điểm BC, O là trung điểm AD. Chứng minh 2OM = AH

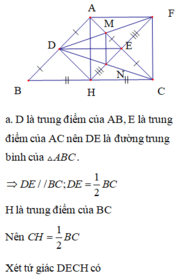


a, △ABC△ABC có: D là trung điểm của BCBC, E là trung điểm của AC
⇒DE là đường trung bình của △ABC
⇒{DE=12AB(1)DE//AB(2)
(1)⇒DE=12.6=3
b, Có: FF là điểm đối xứng với DD qua EE
⇒DE=DF
⇒DF=2DE=2.12AB=AB(3)
(theo (1)(2),(3)⇒ABDF(2),(3)⇒ABDF là hình bình hành □◻
c, ABDF là hình bình hành ⇒{AF//BD(4)AF=BD
Mặt khác D là trung điểm của BC nên BD=BC ⇒AF=BC(5)
(4),(5)⇒ADCF là hình bình hành
Ta lại có: {AB⊥AC(ˆA=90∘)AB//DF⇒AC⊥DF
Vậy hình bình hành ADCFcó hai đường chéo vuông góc hay là ADCFlà hình thoi
Có ADCF là hình thoi ⇒AE=12AC=4
△ADE có ˆE=90∘ (AC⊥DF)
⇒AE2+DE2=AD2(Định lý Pythagore)
thay AE=4AE=4 và DE=3DE=3 tính được AD=√42+32=√25=5
d, Để ADCF là hình vuông thì AD⊥BC
Mà có DC=DB=12BC(gt) nên AD⊥BC khi và chỉ khi AD là đường trung trực của BC
Tức là AB=AC hay △ABC vuông cân tại A
Điều kiện để ADCF là hình vuông là △ABC vuông cân tại A
sai thì thôi nha
thank nhiều