Câu1: Giải phương trình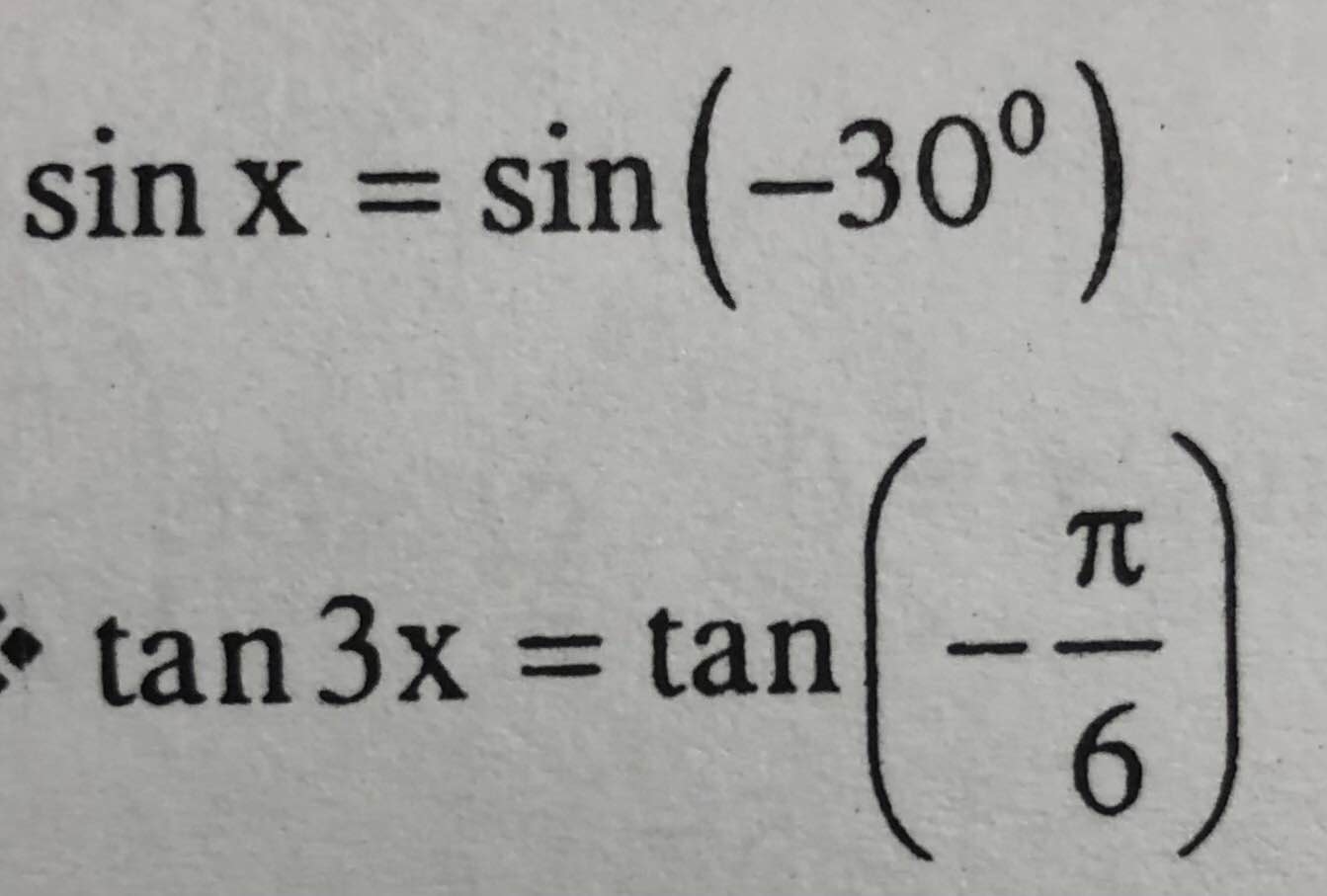
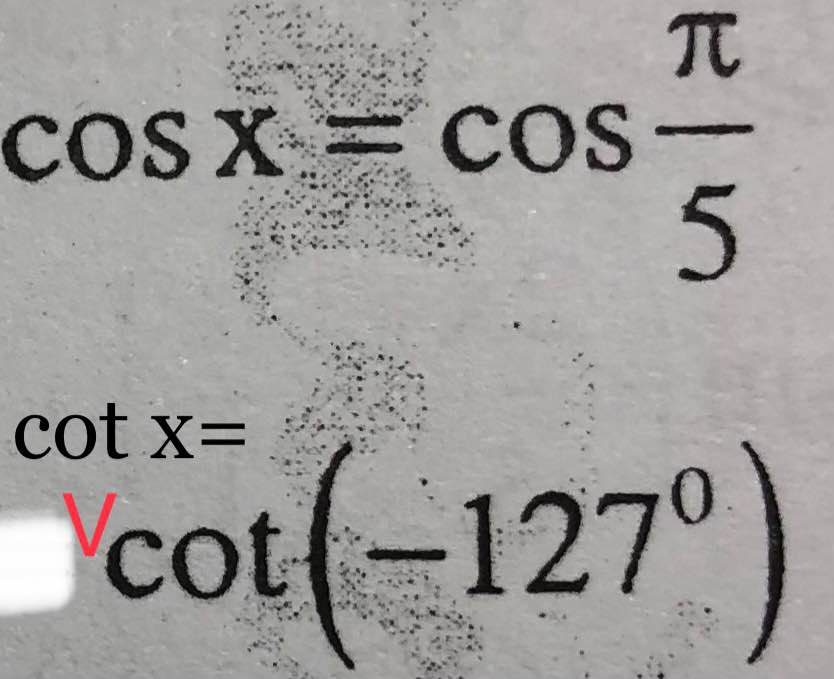
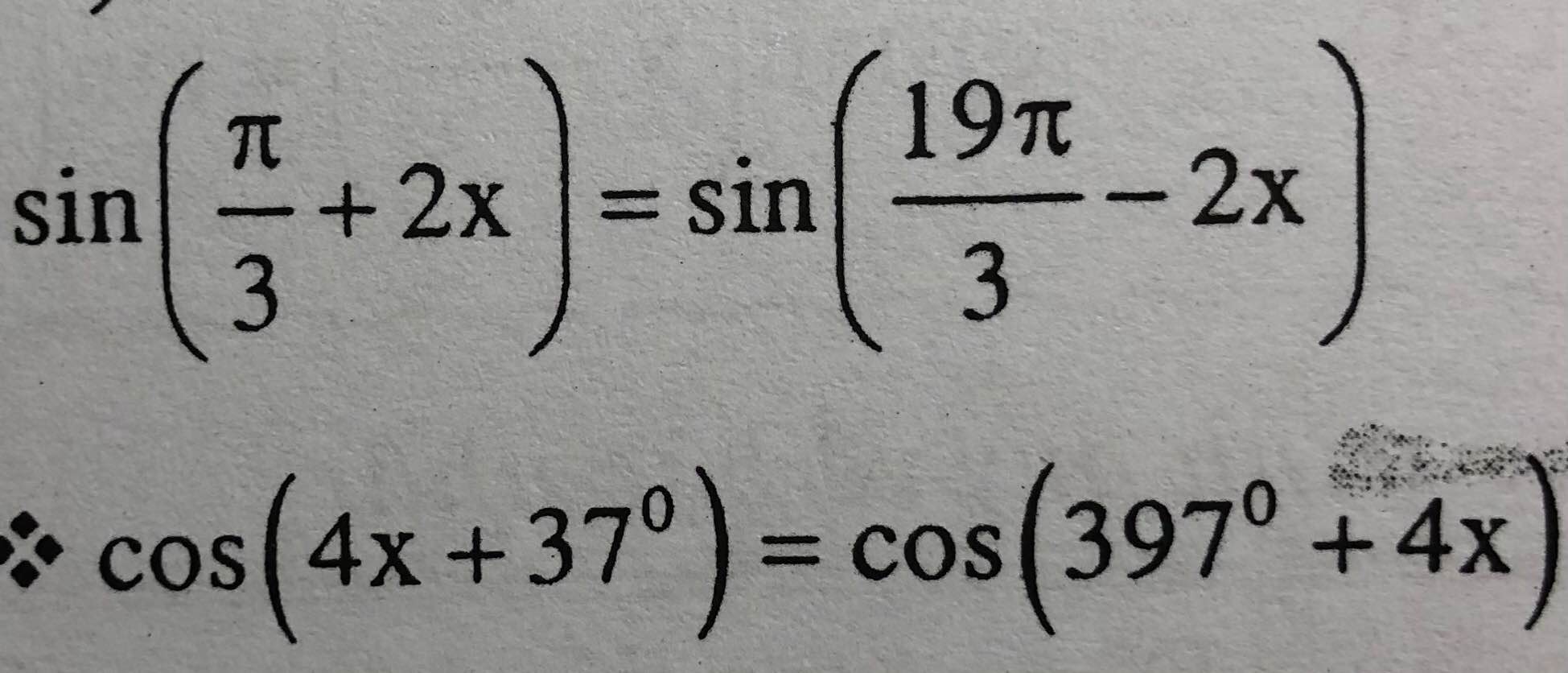
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi chiều dài ban đầu của mảnh vườn là: a (m) ( a thuộc N*)
=> Chiều rộng ban đầu của mảnh vườn là: a - 20 (m)
S lúc đầu của mạnh vườn là: a.(a-20) = a2 - 20a (m2)
Chiều dài sau khi tăng lên của mảnh vườn là: a + 15 (m)
Chiều rộng sau khi giảm của mảnh vườn là: (a-20)-2 = a-22 (m)
Vì nếu tăng chiều dài 15m và giảm chiều rộng đi 2m thì diện tích tăng 60m(vuông) nên ta có phương trình:
S lúc sau của mạnh vườn là: (a+15)(a-22) = a2 - 20a + 60 (m2)
<=> a2 -7a-330 = a2 - 20a + 60
<=> 13a = 390
<=> a = 30 (TM)
Vậy S lúc đầu của mạnh vườn là: 302 - 20. 30 = 300 (m2)

1 - B
\(2x-4=0\)
\(\Leftrightarrow2x=4\)
\(\Leftrightarrow x=2\)
2 - B
| QĐ | VT | TG |
| \(10x\) | \(10\) | \(x\) |

a) \(2\chi-3=3\left(\chi+1\right)\)
\(\Leftrightarrow2\chi-3=3\chi+3\)
\(\Leftrightarrow2\chi-3\chi=3+3\)
\(\Leftrightarrow\chi=-6\)
Vậy phương trình có tập nghiệm S= \(\left\{-6\right\}\)
\(3\chi-3=2\left(\chi+1\right)\)
\(\Leftrightarrow3\chi-3=2\chi+2\)
\(\Leftrightarrow3\chi-2\chi=2+3\)
\(\Leftrightarrow\chi=5\)
Vậy phương trình có tập nghiệm S= \(\left\{5\right\}\)
b) \(\left(3\chi+2\right)\left(4\chi-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3\chi+2=0\\4\chi-5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3\chi=-2\\4\chi=5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\chi=\dfrac{-2}{3}\\\chi=\dfrac{5}{4}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm S= \(\left\{\dfrac{-2}{3};\dfrac{5}{4}\right\}\)
\(\left(3\chi+5\right)\left(4\chi-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3\chi+5=0\\4\chi-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3\chi=-5\\4\chi=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\chi=\dfrac{-5}{3}\\\chi=\dfrac{1}{2}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm S= \(\left\{\dfrac{-5}{3};\dfrac{1}{2}\right\}\)
c) \(\left|\chi-7\right|=2\chi+3\)
Trường hợp 1:
Nếu \(\chi-7\ge0\Leftrightarrow\chi\ge7\)
Khi đó:\(\left|\chi-7\right|=2\chi+3\)
\(\Leftrightarrow\chi-7=2\chi+3\)
\(\Leftrightarrow\chi-2\chi=3+7\)
\(\Leftrightarrow\chi=-10\) (KTMĐK)
Trường hợp 2:
Nếu \(\chi-7\le0\Leftrightarrow\chi\le7\)
Khi đó: \(\left|\chi-7\right|=2\chi+3\)
\(\Leftrightarrow-\chi+7=2\chi+3\)
\(\Leftrightarrow-\chi-2\chi=3-7\)
\(\Leftrightarrow-3\chi=-4\)
\(\Leftrightarrow\chi=\dfrac{4}{3}\)(TMĐK)
Vậy phương trình có tập nghiệm S=\(\left\{\dfrac{4}{3}\right\}\)
\(\left|\chi-4\right|=5-3\chi\)
Trường hợp 1:
Nếu \(\chi-4\ge0\Leftrightarrow\chi\ge4\)
Khi đó: \(\left|\chi-4\right|=5-3\chi\)
\(\Leftrightarrow\chi-4=5-3\chi\)
\(\Leftrightarrow\chi+3\chi=5+4\)
\(\Leftrightarrow4\chi=9\)
\(\Leftrightarrow\chi=\dfrac{9}{4}\)(KTMĐK)
Trường hợp 2: Nếu \(\chi-4\le0\Leftrightarrow\chi\le4\)
Khi đó: \(\left|\chi-4\right|=5-3\chi\)
\(\Leftrightarrow-\chi+4=5-3\chi\)
\(\Leftrightarrow-\chi+3\chi=5-4\)
\(\Leftrightarrow2\chi=1\)
\(\Leftrightarrow\chi=\dfrac{1}{2}\)(TMĐK)
Vậy phương trình có tập nghiệm S=\(\left\{\dfrac{1}{2}\right\}\)

1: Xét tứ giác AEHF có
góc AEH+góc AFH=180 độ
nên AEHF là tứ giác nội tiếp
Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
nên BFEC là tứ giác nội tiếp
=>góc BFE+góc BC=180 độ
=>góc QFB=góc QCE
mà góc Q chung
nên ΔQFB đồng dạng với ΔQCE
=>QF/QC=QB/QE
=>QF*QE=QB*QC

a)\(CuO+H_2\xrightarrow[]{}Cu+H_2\)
b)\(Zn+H_2SO_4\xrightarrow[]{}ZnSO_4+H_2\)
c)\(Al+AgNO_3\xrightarrow[]{}Al\left(NO_3\right)_3+Ag\)
d)\(2Na+2H_2O\xrightarrow[]{}2NaOH+H_2\)
e)\(Na_2O+H_2\xrightarrow[]{}NaOH\)
f)\(2KClO_3\xrightarrow[]{t^0}2KCl+3O_2\)
a, \(CuO+H_2\underrightarrow{t^o}Cu+H_2O\) - pư thế
b, \(Zn+H_2SO_4\rightarrow ZnSO_4+H_2\) - pư thế
c, \(Al+3AgNO_3\rightarrow Al\left(NO_3\right)_3+3Ag\) - pư thế
d, \(2Na+2H_2O\rightarrow2NaOH+H_2\) - pư thế
e, \(Na_2O+H_2O\rightarrow2NaOH\) - pư hóa hợp
f, \(2KClO_3\underrightarrow{t^o}2KCl+3O_2\) - pư phân hủy


a.
\(sinx=sin\left(-30^0\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-30^0+k360^0\\x=210^0+k360^0\end{matrix}\right.\)
b.
\(tan3x=tan\left(-\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow3x=-\dfrac{\pi}{6}+k\pi\)
\(\Leftrightarrow x=-\dfrac{\pi}{18}+k\pi3\)
c.
\(cosx=cos\left(\dfrac{\pi}{5}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{5}+k2\pi\\x=-\dfrac{\pi}{5}+k2\pi\end{matrix}\right.\)
d.
\(cotx=cot\left(-127^0\right)\)
\(\Leftrightarrow x=-127^0+k180^0\)
e.
\(sin\left(\dfrac{\pi}{3}+2x\right)=sin\left(\dfrac{19\pi}{3}-2x\right)\)
\(\Leftrightarrow sin\left(\dfrac{\pi}{3}+2x\right)=sin\left(\dfrac{\pi}{3}-2x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{\pi}{3}+2x=\dfrac{\pi}{3}-2x+k2\pi\\\dfrac{\pi}{3}+2x=\dfrac{\pi}{6}+2x+k2\pi\left(vn\right)\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{k\pi}{2}\)