Giúp mình với ạ
CMR: Đồị của hàm số y= ax2 và đồ thị của hàm số y= ax2 +bx+c (a khác 0) tương tự nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 7 2019
Với a = 1; b = -1, hàm số trở thành: y = x 3 + x 2 – x + 1.
- Tập xác định : D = R.
- Sự biến thiên :
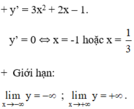
+ Bảng biến thiên :
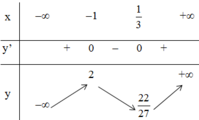
Kết luận :
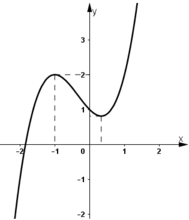
Hàm số đồng biến trên (-∞ ; -1) và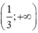 
Hàm số nghịch biến trên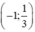 
Hàm số đạt cực đại tại x = -1 ; yCĐ = 2.
Hàm số đạt cực tiểu tại 
- Đồ thị :
CM
6 tháng 10 2019
Ta có: x = − b 2 a > 0 nên trục đối xứng nằm bên phải trục Oy
Đồ thị cắt trục tung tại điểm (0; c) nằm dưới trục hoành ( vì c < 0).
Do đó, đồ thị B là đồ thị của hàm số đã cho.
Đáp án B
CM
25 tháng 6 2018
Đáp án C.
lim x → - ∞ y = - ∞ ( 1 ) f ( - 1 ) = - 1 + a 2 - b + c > 0 ( 2 ) f ( 2 ) = 8 + 4 a 2 + 2 a + c < 0 ( 3 ) lim x → - ∞ y = + ∞ ( 4 )
Từ (1) và (2) ⇒ Phương trình f (x) = 0 có ít nhất một nghiệm trên - ∞ ; - 1 .
Từ (2) và (3) ⇒ Phương trình f (x) = 0 có ít nhất một nghiệm trên - 1 ; 2 .
Từ (3) và (4) ⇒ Phương trình f (x) = 0 có ít nhất một nghiệm trên 2 ; + ∞ .
Do f (x) =0 là phương trình bậc 3 ⇒ Có nhiều nhất 3 nghiệm
⇒ Đường thẳng cắt trục Ox tại 3 điểm phân biệt.
CM
28 tháng 7 2019
Đáp án C
Phương pháp giải:
Chọn hệ số a, b, c hoặc đánh giá tích để biện luận số nghiệm của phương trình
Lời giải:
Cách 1. Ta có: 
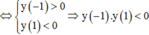
Lại có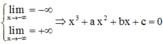 
có 3 nghiệm thuộc khoảng 
Cách 2. Chọn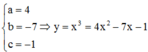 
và đồ thị hàm số cắt trục Ox tại 3 điểm phân biệt
17 tháng 2 2022
a, y = ax^2 đi qua B(2;4)
<=> 4a = 4 <=> a = 1
b, bạn tự vẽ
17 tháng 2 2022
a: Thay x=2 và y=4 vào hàm số, ta được:
\(a\cdot4=4\)
hay a=1
b: Thay x=2 và y=4 vào hàm số, ta được:
4a=4
hay a=1
Đặt (P) : y = ax2
(P') : y = ax2+bx+c
Ta có : (P') : \(y=ax^2+bx+c=a\left(x^2+\frac{2.x.b}{2a}+\frac{b^2}{4a^2}-\frac{b^2}{4a^2}\right)+c\)
\(=a\left(x+\frac{b}{2a}\right)^2+c-\frac{b^2}{4a}=a\left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{4a}\)
Đặt \(p=\frac{b}{2a}\) , \(q=-\frac{b^2-4ac}{4a}\) thì khi đó
\(\left(P'\right):y=a\left(x+p\right)^2+q\)
Điều này có nghĩa là ta tịnh tiến (P) sang phải p đơn vị , tịnh tiến lên trên q đơn vị thì được (P') => (P') thực chất là "phép tịnh tiến" của (P)
Từ đó bạn rút ra được điều phải chứng minh nhé!
Cách chứng minh trong SGK có viết rất rõ rồi , bạn tham khảo nhé !
Mình quên mất ,bạn chú ý rằng các giá trị a,b,c chưa xác định do vậy ta chỉ cần nói (P') là phép tịnh tiến của (P) thôi nhé, còn trái phải lên xuống chưa rõ ^^