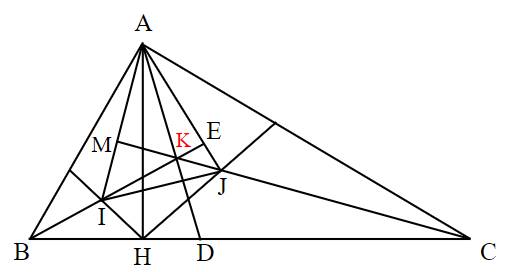
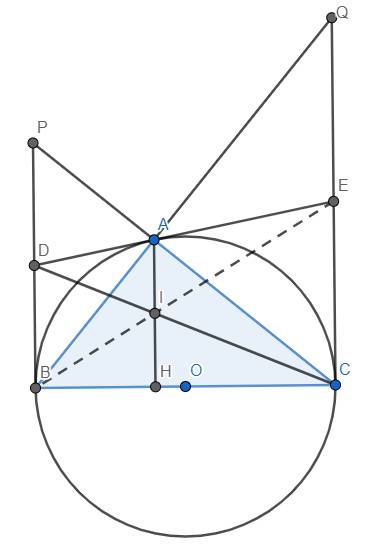
Cho tam giác ABCABC vuông tại AA, đường cao AHAH. Gọi II và KK theo thứ tự là giao điểm các đường phân giác của tam giác AHBAHB và AHCAHC.
a) Chứng minh rằng BIBI vuông góc với AKAK.
b) Gọi OO là giao điểm của BIBI và CKCK. Điểm OO là giao điểm ba đường nào của tam giác ABCABC ?
c) Điểm OO là giao điểm ba đường nào của tam giác AIKAIK ?
d) Chứng minh rằng AOAO vuông góc với IKIK.