Cho hình thang cân ABCD ( AB // CD ) .Gọi M , N , P , Q theo thứ tự là trug điểm AB , BC , CD , DA
a) C/m tg MNPQ là h.thoi
b) Hình thang cân ABCD cần thêm điều kienj gì để tg MNPQ là hình vuông?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a / hình bình hành
b/ AC=BD ; AB>CD ; AB<AC<CD;AB<BD<CD
c/hình vuông
(Hình thì bạn tự vẽ nha)
a) Xét tam giác BAD có: MB=MA ; QB=QD
=> MQ là đường trung bình của tam giác BAD
=> MQ // AD ; MQ = 1/2 AD (1)
Xét tam giác CAD có: NC = NA ; PC = PD
=> NP là đường trung bình của tam giác CAD
=> NP // AD ; NP = 1/2 AD (2)
Từ (1), (2) => MQ // NP ; MQ = NP
Tứ giác MNPQ có: MQ // NP ; MQ = NP
=> MNPQ là hình bình hành
b) Theo a), ta có: MQ = 1/2 AD (*)
Xét tam giác ABC có: MA = MB ; NA = NC
=>MN là đường trung bình của tam giác ABC
=> MN = 1/2 BC (**)
Từ (*), (**) và AD=BC (ABCD là thang cân)
=> MQ = MN
Hình bình hành MNPQ có MQ = MN
=> MNPQ là hình thoi

(Hình thì bạn tự vẽ nha)
a) Xét tam giác BAD có: MB=MA ; QB=QD
=> MQ là đường trung bình của tam giác BAD
=> MQ // AD ; MQ = 1/2 AD (1)
Xét tam giác CAD có: NC = NA ; PC = PD
=> NP là đường trung bình của tam giác CAD
=> NP // AD ; NP = 1/2 AD (2)
Từ (1), (2) => MQ // NP ; MQ = NP
Tứ giác MNPQ có: MQ // NP ; MQ = NP
=> MNPQ là hình bình hành
b) Theo a), ta có: MQ = 1/2 AD (*)
Xét tam giác ABC có: MA = MB ; NA = NC
=>MN là đường trung bình của tam giác ABC
=> MN = 1/2 BC (**)
Từ (*), (**) và AD=BC (ABCD là thang cân)
=> MQ = MN
Hình bình hành MNPQ có MQ = MN
=> MNPQ là hình thoi

Hình thang ABCD là hình thang cân có hai góc kề một đáy đều bằng 45 0 thì MNPQ là hình vuông.

MNPQ là hình thoi vì là hình bình hành có hai cạnh kề bằng nhau.

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\left(1\right)\)
Xét ΔDBC có
Q là trung điểm của BD
P là trung điểm của CD
Do đó: QP là đường trung bình của ΔDBC
Suy ra: QP//BC và \(QP=\dfrac{BC}{2}\left(2\right)\)
Từ (1) và (2) suy ra MN//PQ và MN=PQ
hay MNPQ là hình bình hành


a.Ta co
la duong trung binh cua tam giac ABD
=> MQ//BD, MQ= 0,5BD (1)
Ta lai co NP la dg trung binh cua tam giac BCD
=> NP//BD, NP=0,5 BD (2)
Tu (1) va (2)=> MNPQ la hinh binh hanh
Ta lai co QP=0,5 AC (vi la dg trung binh)
ma ABCD la hinh thang can => AC=BD=> MQ=QP
=>MNQP la hinh thoi

Tam giác BCD có :
BN = NC ( gt )
DP = PC ( gt )
\(\Rightarrow\)NP là đường trung bình tam giác BCD ( 1 )
Tam giác ADB có :
AQ = QD ( gt )
AM = MB ( gt )
\(\Rightarrow\)QM là đường trung bình tam giác ADB ( 2 )
Từ ( 1 ) , ( 2 ) suy ra NP = QM , NP // QM
\(\Rightarrow\)MNEF là hình bình hành ( đến đây bạn tự chứng minh tiếp hình thoi )
c) Để MNPQ là hình vuông thì ta chứng minh ABCD là hình thang cân có 2 đường chéo vuông góc với nhau
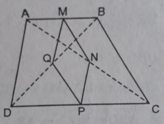
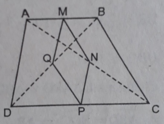
a,
Xét ABD, ta có :
MA = MB (gt)
QA = QD (gt)
=> MQ là đường trung bình.
=> MQ // BD và MQ = BD : 2 (1)
Cmtt, ta được :
NP // BD và NP = BD : 2 (2)
NM // AC và NM = AC : 2 (3)
Từ (1) và (2) : MQ // NP và MQ = PP
=> Tứ giác MNPQ làhình bình hành.
ta có :
AC = BD ( hai đường chéo hình thang cân ABCD)
NM = AC : 2 (cmt)
MQ = BD : 2 (cmt)
=> NM = MQ
Xét hình bình hành MNPQ, ta có :
NM = MQ (cmt)
=> hình bình hành MNPQ là hình thoi.
b , Nếu AC BD
BD
NM // AC (cmt)
NP // BD (cmt)
=> NM NP tại N
NP tại N
Hay
Xét hình thoi MNPQ , ta có : (cmt)
(cmt)
=> hình thoi MNPQ là hình vuông.
tick nha bn