Để tính vị trí của vật điều hoà tại thời điểm 1/3 giây sau khi vật có li độ x = 3cm, chúng ta cần tính giá trị của x tại thời điểm đó.

Phương trình vật dao động điều hoà đã cho là: x = 6cos(2πt - π/6) (cm)

Để tìm thời điểm 1/3s tiếp theo, ta thay t = 1/3 vào phương trình trên:

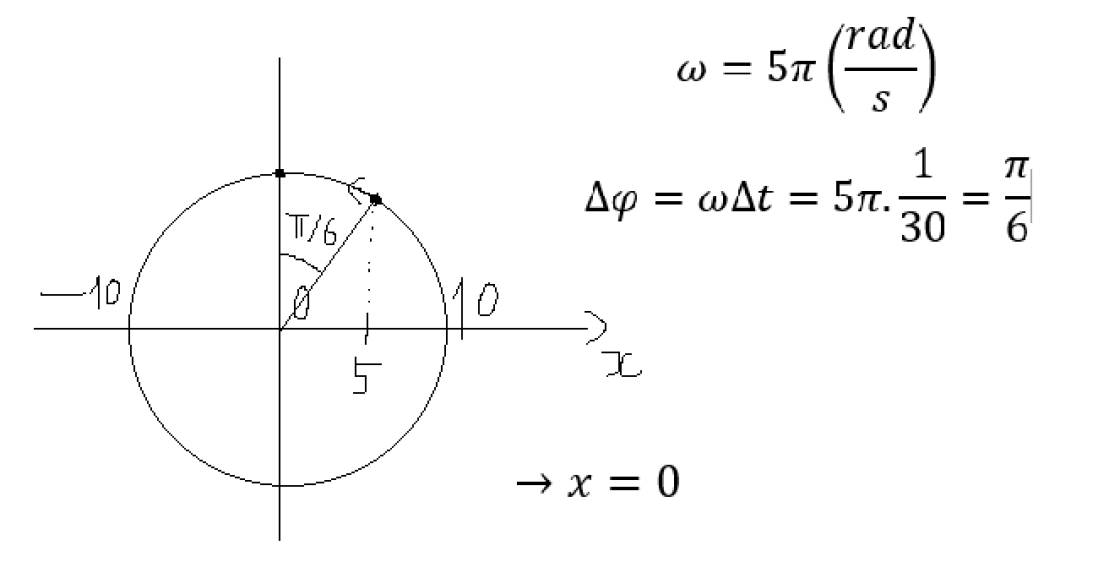
x = 6cos(2π(1/3) - π/6) = 6cos(2π/3 - π/6) = 6cos(π/2) = 6 * 0 = 0 (cm)

Vậy, tại thời điểm 1/3s tiếp theo, vật sẽ ở li độ x = 0cm.

Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{4\pi}=0,5s\)

Ta có: \(x=2,5\sqrt{2}=\dfrac{A\sqrt{2}}{2}\) và đang có xu hướng giảm.

Lúc này vật ở thời điểm: \(t_1=\dfrac{T}{8}\)

Tại thời điểm: \(t=\dfrac{7}{48}s=\dfrac{7T}{14}=\dfrac{T}{8}+\dfrac{T}{6}\)

Dựa vào vòng tròn lượng giác \(\Rightarrow x=2,5cm\)

Hình vẽ đây nha

Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=0,5s\)

a) t = 0,124s = T/4

Biểu diễn dao động bằng véc tơ quay, ta có:

Ban đầu, vị trí của vật ứng với véc tơ quay tại M, sau T/4, vị trí đó đến điểm N.

\(\Rightarrow x = 8\cos 30^0=4\sqrt 3(cm)\)

b) Hoàn toàn tương tự, ta tìm được li độ của vật sau 0,3125s là \(x=0cm\)

Đáp án A

Theo mình là câu D bạn nhé vì từ pt suy ra được tần số gốc là pi:3 mà T=2pi:tần số gốc => T=6s Tại t1 có x=2cm Vậy t1+6=t1+T nên sau khi đi 1 chu kì vẫn quay lại vị trí x=2cm

Phương trình dạo động là: \(x=4cos\left(2\pi t+\dfrac{\pi}{3}\right)cm\)

Chu kì dao động là: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{2\pi}=1\left(s\right)\Rightarrow0,25=\dfrac{T}{4}\)

Tại thời điểm t₁, vật có li độ đang giảm và có giá trị 2cm

\(\Rightarrow\Delta\varphi=\dfrac{\pi}{3}\)

Tại thời điểm t₂ = t₁ + 0,25, vật quay một góc \(\dfrac{\pi}{2}\) so với thời điểm t₁.

\(\Rightarrow x_2=-\dfrac{A\sqrt{3}}{2}=-\dfrac{4\sqrt{3}}{2}=-2\sqrt{3}\left(cm\right)\)

Chọn A.

Ta có:

-  Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{4\pi}=0,5s\)

\(\Delta t=t_1-t_2=\dfrac{7}{48}s\)

Góc vật quét được khi từ thời điểm \(t_1\) đến \(t_2\) : \(\Delta\varphi=\omega\Delta t=4\pi.\dfrac{7}{48}=105^o\)

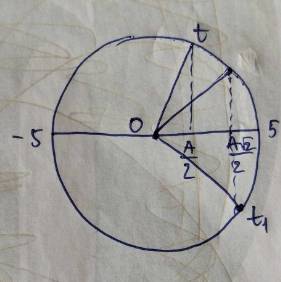
Tại thời điểm \(t_1\) vật đang có li độ: \(x=5\left(cm\right)=\dfrac{A}{2}\)

+ Với \(t_1\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_1\left(2\right)\)

\(x_1=A.sin\left(15^o\right)=2,59cm\)

+ Với \(t_2\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_2\left(2\right)\)

\(x_2=A.cos\left(15^o\right)=9,66\left(cm\right)\)\(\Rightarrow A\)