Cho goc nhon xOy. Lấy điểm A thuộc tiia Ox, lấy điểm B thuộc tia Oy sao cho OA=OB. Qua A kẻ đường thẳng vuông góc với tia Ox cắt tia Oy tại M, qua B kẻ đường thẳng vuông góc với tia Oy cắt tia Ox tại N. Gọi H là giao điểm của AM và BN, I là trung điểm của MN. CMR
a/ ON=OM
b/ Ba điểm O, H, I thẳng hàng
giup vs nk

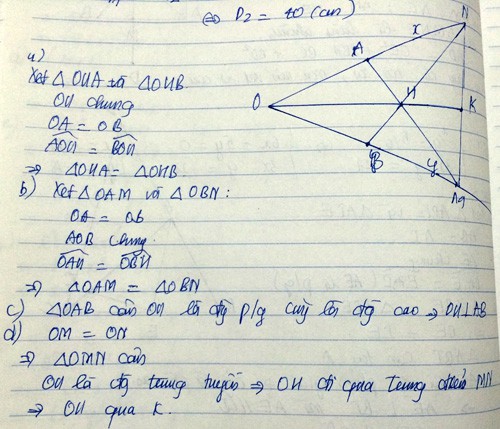
a: Xét ΔOAM vuông tại A và ΔOBN vuông tại B có
OA=OB
\(\widehat{AOM}\) chung
Do đó: ΔOAM=ΔOBN
Suy ra OM=ON
b: Xét ΔBHM vuông tại B và ΔAHN vuông tại A có
BM=AN
\(\widehat{BHM}=\widehat{AHN}\)
Do đó: ΔBHM=ΔAHN
Suy ra: HN=HM
mà OM=ON
và IM=IN
nên O,H,I thẳng hàng