3a^2-b^2/a^2+b^2=3/4 tính a/b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow12a^2-4b^2=3a^2+3b^2\)
\(\Leftrightarrow9a^2=7b^2\)
\(\Leftrightarrow\dfrac{a^2}{b^2}=\dfrac{7}{9}\)
hay \(\dfrac{a}{b}\in\left\{\dfrac{\sqrt{7}}{3};-\dfrac{\sqrt{7}}{3}\right\}\)
\(\dfrac{3a^2-b^2}{a^2+b^2}=\dfrac{3}{4}\)
\(\Leftrightarrow4.\left(3a^2-b^2\right)=3\left(a^2+b^2\right)\)
\(\Leftrightarrow12a^2-4b^2=3a^2+3b^2\)
\(\Leftrightarrow12a^2-3a^2=3b^2+4b^2\)
\(\Leftrightarrow9a^2=7b^2\)
\(\Leftrightarrow\dfrac{a^2}{b^2}=\dfrac{7}{9}\)
\(\text{hoặc }\dfrac{a}{b}=\pm\dfrac{\sqrt{7}}{3}\)


Ta có công thức tổng quát như sau:
\(A=n^k+n^{k+1}+n^{k+2}+...+n^{k+x}\Rightarrow A=\dfrac{n^{k+x+1}-n^k}{n-1}\)
Áp dụng ta có:
\(A=1+4+4^2+...+4^6=\dfrac{4^7-1}{3}\)
\(\Rightarrow B-3A=4^7-3\cdot\dfrac{4^7-1}{3}=1\)
______
\(A=2^0+2^1+...+2^{2008}=2^{2009}-1\)
\(\Rightarrow B-A=2^{2009}-2^{2009}+1=1\)
_____
\(A=1+3+3^2+....+3^{2006}=\dfrac{3^{2007}-1}{2}\)
\(\Rightarrow B-2A=3^{2007}-2\cdot\dfrac{3^{2007}-1}{2}=1\)

a: \(A=-2y^3-3y^4+2\)
\(B=7y^4+2y^3+3y^2-3y-3\)
b: \(A+B=4y^4+3y^2-3y-1\)
\(A-B=-10y^4-4y^3-3y^2+3y+5\)

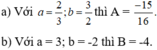
theo bài ra ta có:
\(\frac{3a^2-b^2}{a^2+b^2}=\frac{3}{4}\)
=> 4( 3a2 - b2) = 3( a2+ b2)
=> 12a2- 4b2 = 3a2 + 3b2
=> 12a2- 3a2 = 3b2 + 4b2
=> 9a2= 7b2
=> \(\frac{7}{9}=\frac{a^2}{b^2}\Rightarrow\sqrt{\frac{7}{9}}=\frac{a}{b}\)
vậy \(\sqrt{\frac{7}{9}}=\frac{a}{b}\)