Cho mạch điện như hình vẽ trong đó r1=15,r2=r3=r4=30 biết cường độ dòng điện qua r2 là i2=0.50 a)tính điện trở của đoạn mạch MP b)tính cường độ dòng điện qua mỗi điện trở c) tính hiệu điện thế của mỗi điện trở và hiệu điện thế giữa 2 điểm MP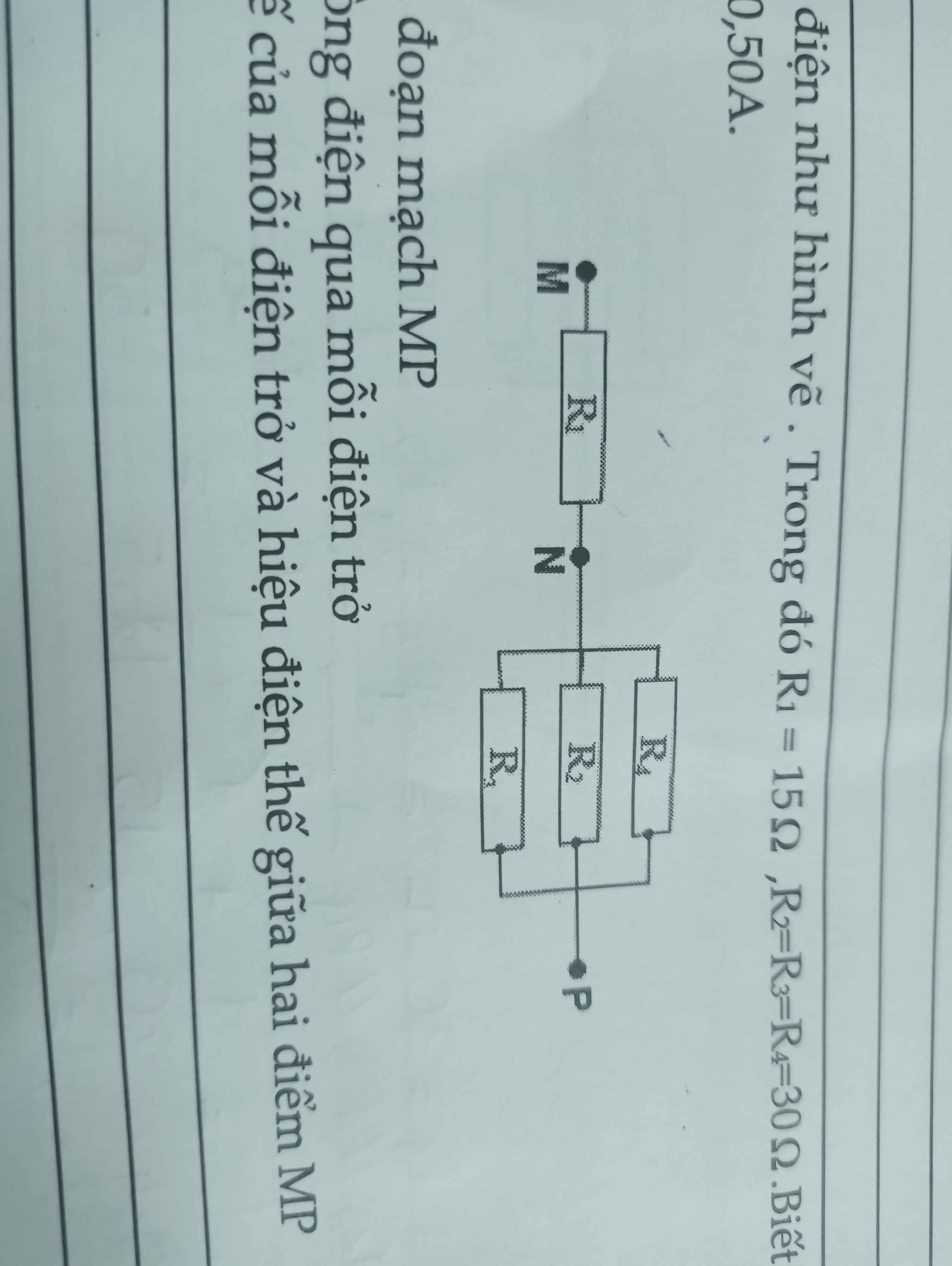
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Rightarrow\left\{{}\begin{matrix}a,R1//\left(R2ntR3\right)\Rightarrow Rtd=\dfrac{R1\left(R2+R3\right)}{R1+R2+R3}=6\Omega\\b,\Rightarrow\left\{{}\begin{matrix}U=U1=U23=24V\Rightarrow I1=\dfrac{U1}{R1}=\dfrac{8}{3}A\\I2=I3=\dfrac{U23}{R2+R3}=\dfrac{4}{3}A\\U2=I2.R2=8V\\U3=U-U2=16V\end{matrix}\right.\\c,R1//\left(R2ntRx\right)\Rightarrow Im=1,5.\dfrac{24}{6}=6A\\\Rightarrow Rtd=\dfrac{R1\left(R2+Rx\right)}{R1+R2+Rx}=\dfrac{9\left(6+Rx\right)}{15+Rx}=\dfrac{24}{Im}=4\left(\Omega\right)\Rightarrow Rx=1,2\Omega\end{matrix}\right.\)

\(R_{12}=\dfrac{15.30}{15+30}=10\left(\Omega\right)\)
\(R_m=R_{12}+R_3=10+30=40\left(\Omega\right)\)
\(I_m=\dfrac{U_{AB}}{R_m}=\dfrac{12}{40}=0,3\left(A\right)\)
\(b,I_{12}=I_3=0,3\left(A\right)\)
\(\dfrac{I_1}{I_2}=\dfrac{R_2}{R_1}=\dfrac{30}{15}=\dfrac{2}{1}\)
\(\rightarrow I_1=0,2\left(A\right);I_2=0,1\left(A\right)\)

mà thôi toi thấy được hình rồi
R1 nt {R2//\([R3nt\left[R4//R5\right]]\)}
a,\(\)\(=>Rtd=R1+\dfrac{R2\left\{R3+\dfrac{R4.R5}{R4+R5}\right\}}{R2+R3+\dfrac{R4R5}{R4+R5}}=80+\dfrac{36\left\{24+\dfrac{6.1}{6+1}\right\}}{36+24+\dfrac{6.1}{6+1}}\)
\(=95\left(ôm\right)\)
b,\(=>I1=I2345=\dfrac{U}{Rtd}=\dfrac{15}{95}=\dfrac{3}{19}A\)
\(=>U2345=U2=U345=\dfrac{3}{10}.R2345=28,4V=>I2=\dfrac{U2}{R2}=0,8A\)
\(=>I345=I3=I45=\dfrac{28,4}{R345}=1,2A\)
(kết quả sấp xỉ thế nhỉ, bn tính toán kĩ lại hộ mình nhé

a. \(R=\dfrac{\left(R1+R2\right)R3}{R1+R2+R3}=\dfrac{\left(80+40\right)60}{80+40+60}=40\Omega\)
b. \(U=U12=U3=IR=40.0,15=6V\)(R12//R3)
\(\left\{{}\begin{matrix}I3=U3:R3=6:60=0,1A\\I12=I1=I2=U12:R12=6:\left(80+40\right)=0,05A\left(R1ntR2\right)\end{matrix}\right.\)

\(MCD:\left(R2//R3\right)ntR1\)
\(\rightarrow R=\dfrac{R2\cdot R3}{R2+R3}+R1=\dfrac{10\cdot12}{10+12}+10=\dfrac{170}{11}\Omega\)
\(I=I1=I23=U:R=24:\dfrac{170}{11}=\dfrac{132}{85}A\)
\(\rightarrow U1=I1\cdot R1=\dfrac{132}{85}\cdot10=\dfrac{264}{17}V\)
\(\rightarrow U23=U2=U3=U-U1=24-\dfrac{264}{17}=\dfrac{144}{17}V\)
\(\rightarrow\left\{{}\begin{matrix}I2=U2:R2=\dfrac{144}{17}:10=\dfrac{72}{85}A\\I3=U3:R3=\dfrac{144}{17}:12=\dfrac{12}{17}A\end{matrix}\right.\)
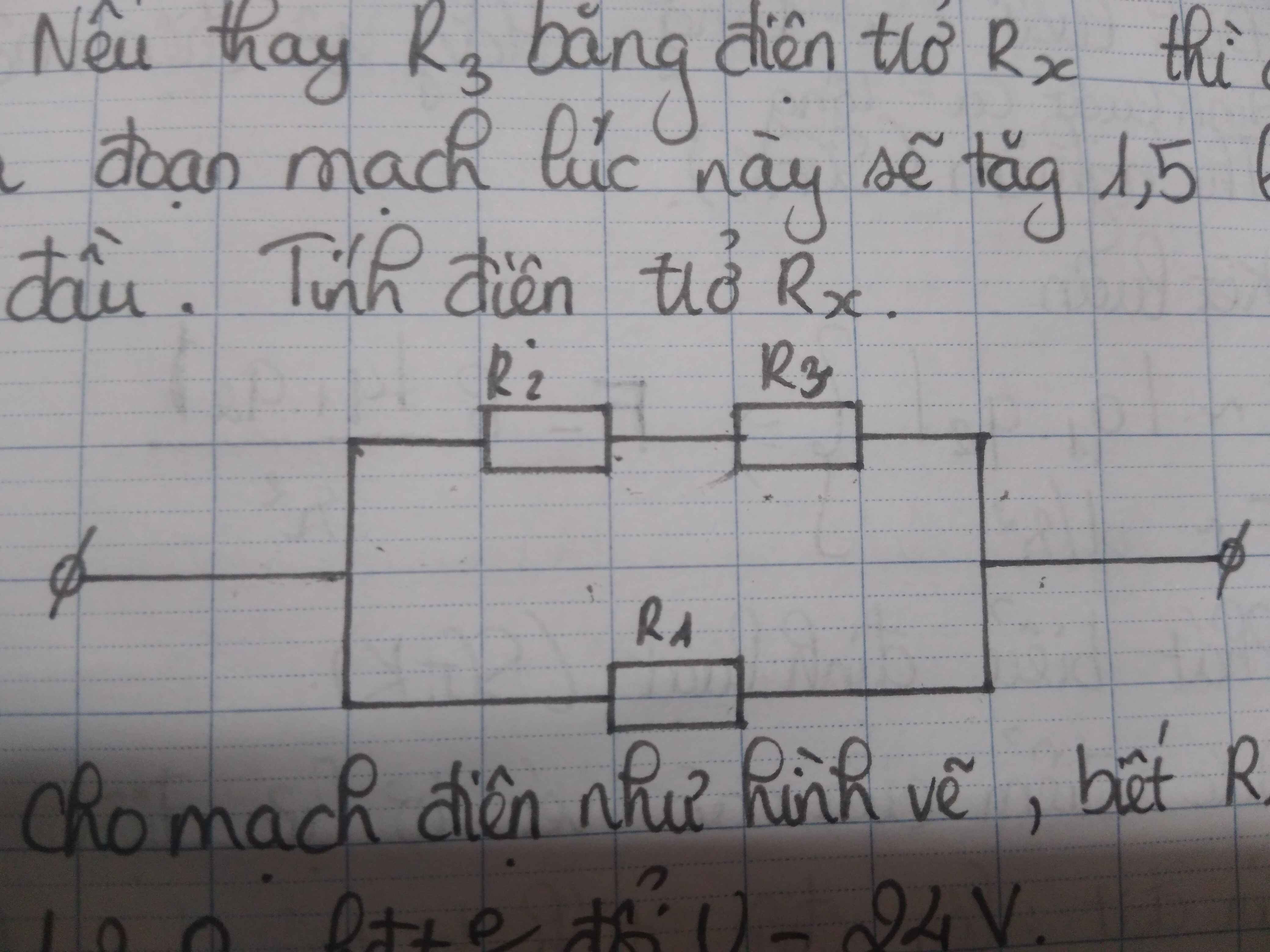

R1 n t (R2//R3//R4)
a,\(=>\dfrac{1}{R234}=\dfrac{1}{R2}+\dfrac{1}{R3}+\dfrac{1}{R4}=>R234=10\left(om\right)\)
\(=>Rmp=R1+R234=25\left(ôm\right)\)
b
ta thấy R2=R3=R4 mà U2=U3=U4
=>I2=I3=I4=0,5A
\(=>I1=I2+I3+I4=1,5A\)
c,\(U2=U3=U4=I2.R2=15V\)
\(U1=I1.R1=22,5V=>Ump=U1+U2=37,5V\)