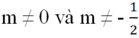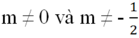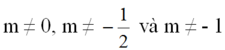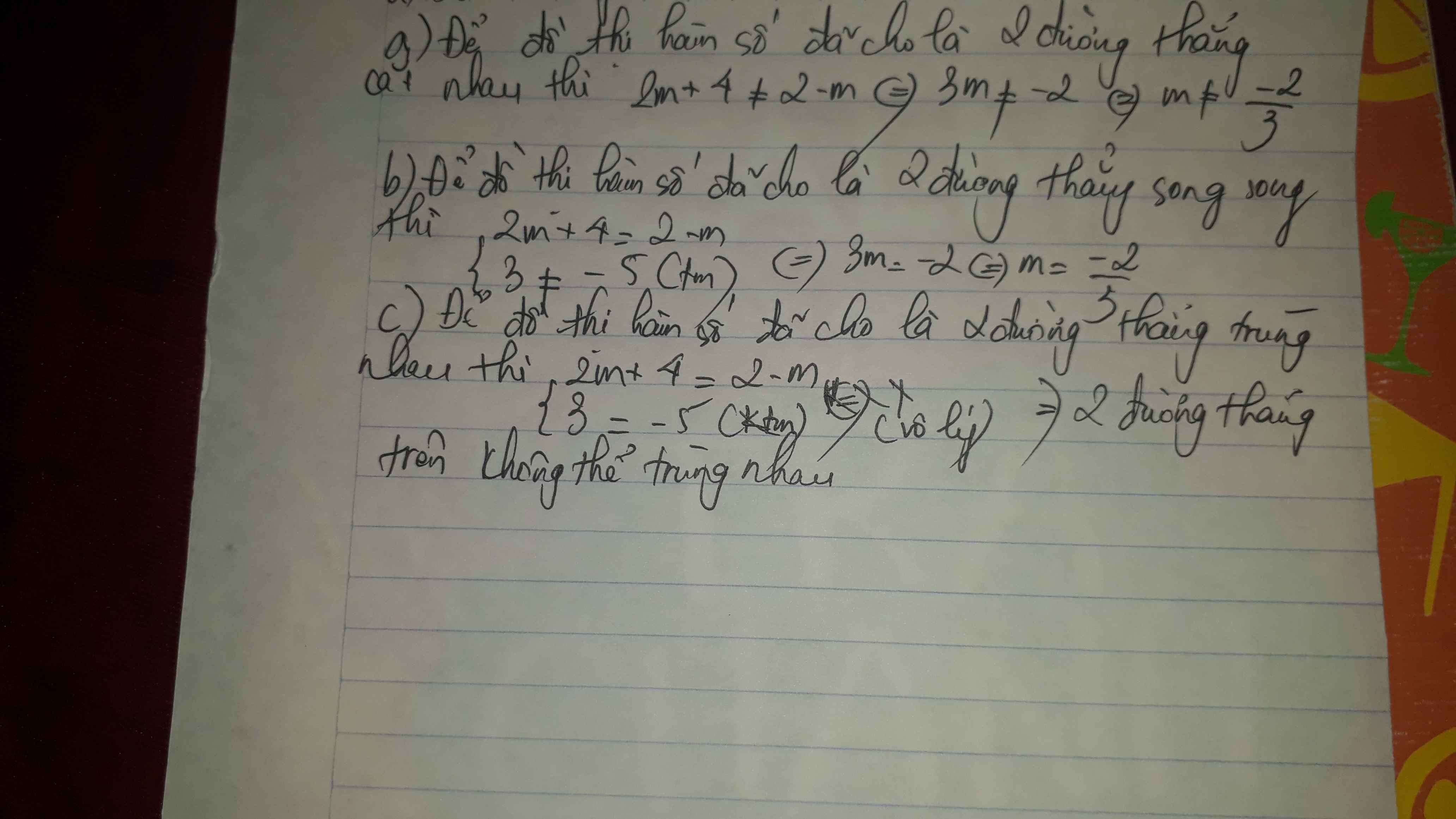Bài 1: Cho hai hàm số bậc nhất
y =mx+3
và
y=(2m+1)x-5
Tìm giá trị của m để đồ thị của hai hàm số đã cho là:
a) Hai đường thẳng song song với nhau. Vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ
với giá trị m vừa tìm được.
b) Hai đường thẳng cắt nhau. Vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ với giá trị m
vừa tìm được.