Bạn tham khảo ở đây nhé:

Câu hỏi của ngô thị gia linh - Toán lớp 7 - Học toán với OnlineMath

 tính số đo góc CAH

Do tia AH nằm giữa 2 tia AB và AC nên:

góc BAH + góc CAH = Góc BAC

35 độ + CAH = 90 độ

=> CAH= 90 - 35 = 55 độ

Xét tam giác ACH có:

góc CAH + góc AHC + góc ACH = 180 độ

55 độ + 90 độ + góc ACH = 180 độ

145 độ + góc ACH =180 độ

=> góc ACH= 180 độ - 145 độ =35 độ

:))) tui nghĩ là zị

ta có: gócHAC= gócA - gocsBAH = 90độ - 35độ = 55độ 

ta có gocsACB = 180độ -gócHAC - góc H

=180 - 55 - 90 35độ

a: AB\(\perp\)AC

HD\(\perp\)AC

Do đó:AB//HD

a) \(\widehat{BAH}=\widehat{C}\) (vì cùng phụ với \(\widehat{B}\))          (1)

   \(\widehat{CAH}=\widehat{B}\) (vì cùng phụ với \(\widehat{C}\))         (2)

Xét tam giác DAB có: \(\widehat{ADC}=\widehat{DAB}+\widehat{B}\)    (vì góc ngoài bằng tổng hai góc trong không kề với nó)

Ta lại có: \(\widehat{DAC}=\widehat{DAH}+\widehat{HAC}\)

Mà \(\widehat{DAB}=\widehat{DAH}\) (tính chất tia phân giác)

      \(\widehat{B}=\widehat{HAC}\) (theo (2))

=> \(\widehat{ADC}=\widehat{DAC}\)

b) Theo câu a ta có: \(\widehat{C}=\widehat{HAB}\)

=> \(\widehat{C_1}=\widehat{C_2}=\widehat{A_1}=\widehat{A_2}\)

Xét tam giác ACK có tổng 2 góc A và C là:

\(\widehat{ACK}+\widehat{CAK}=\widehat{C_2}+\widehat{CAK}=\widehat{A_1}+\widehat{CAK}=\widehat{CAB}=90^o\)

=> Góc còn lại bằng 90 độ, tức là \(\widehat{AKC}=180^o-\left(\widehat{ACK}+\widehat{CAK}\right)=180^o-90^o=90^o\)

=> CK vuông góc với AD

`a)`

`Delta HAC` vuông tại `H` có :`hat(A_1)+hat(ACB)=90^0`

`hat(HAB)+hat(A_1)=90^0(kề bù)`

nên `hat(ACB)=hat(A_1)(đpcm)`

`b)`

`Delta HAC` vuông tại `H` có : `hat(A_1)+hat(ACH)=90^0` 

hay `hat(A_1)+hat(ACB)=90^0`

`Delta ABC` vuông tại `A` có : `hat(B)=hat(ACB)=90^0`

nên `hat(B)=hat(A_1)`

Có `hat(IAC)=hat(A_1)+hat(A_2)`

`=1/2 hat(BAH)+hat(B)=1/2 hat(BCA) +hat(BAH)` (1)

`hat(C_1)=1/2 hat(ACB)(CI` là p/g của `hat(ACB)` `)`(2)

Từ `(1)` và `(2)=>hat(IAC)+hat(C_1)=hat(ABH)+hat(ACB)`

mà `hat(ABH)+hat(ACB)=90^0` 

nên `hat(IAC)+hat(C_1)=90^0`

hay `hat(I_1)=90^0`

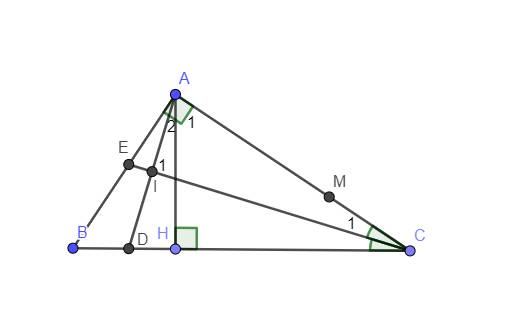
\(\widehat{DAC}+\widehat{DAB}=90^0\)

\(\widehat{ADC}+\widehat{HAD}=90^0\)

mà \(\widehat{BAD}=\widehat{HAD}\)

nên \(\widehat{ADC}=\widehat{DAC}\)