1. BA TRUNG ĐIỂM 3 CẠNH CỦA 1 TAM GIÁC LÀ M1(2;1), M2(5;3), M3(3;-4). TÌM PHƯƠNG TRÌNH 3 CẠNH CỦA TAM GIÁC.
2. CHO P(-2;3). TÌM PHƯƠNG TRÌNH ĐƯỜNG THẲNG QUA P VÀ CÁCH ĐỀU 2 ĐIỂM A(5;-1), B(3;7).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3. Gọi tam giác đó là ABC với góc A vuông, các đường trung trực ứng với cạnh AB, AC lần lượt là MN,PQ; D là trung điểm cạnh huyền AC
Có : MN song song với AC và đi qua M là trung điểm của AB => N là trung điểm của BC(t/c đường trung bình) => N trùng với D
PQ song song với AB và đi qua P là trung điểm của AC => Q là trung điểm của BC(t/c đường trung bình) => Q trùng với D
MN cắt PQ tại trung điểm D của BC
Mà đường trung bình của BC đi qua D
=> Giao điểm 3 đường trung trực là D trung điểm cạnh huyền BC

Đáp án B
Tam giác đều cạnh x có bán kính đường tròn ngoại tiếp là
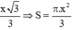
Với mỗi tam giác đề bài cho, độ dài cạnh tam giác sau bẳng 1 2 độ dài cạnh tam giác trước.
Khi đó
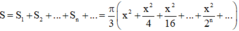
Dễ thấy
![]()
là tổng cấp số nhân lùi vô hạn
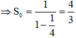
Vậy tổng cần tính là
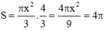

1: Xét ΔBAM và ΔBNM có
BA=BN
góc ABM=goc NBM
BM chung
Do đó: ΔBAM=ΔBNM
2: ΔBAM=ΔBNM
=>MA=MN
mà BA=BN
nên BM là trung trực của AN
=>I là trung điểm của AN
3: góc ABC+góc C=90 độ
góc NMC+góc C=90 độ
=>góc ABC=góc NMC

M là trung điểm của BC
=>\(\left\{{}\begin{matrix}x_B+x_C=2\cdot x_M=2\cdot2=4\\y_B+y_C=2\cdot y_M=2\cdot3=6\end{matrix}\right.\)(1)
N là trung điểm của AC
=>\(\left\{{}\begin{matrix}x_A+x_C=2\cdot x_N=2\cdot4=8\\y_A+y_C=2\cdot y_N=2\cdot\left(-1\right)=-2\end{matrix}\right.\left(2\right)\)
P là trung điểm của AB
=>\(\left\{{}\begin{matrix}x_A+x_B=2\cdot x_P=2\cdot\left(-3\right)=-6\\y_A+y_B=2\cdot y_P=2\cdot5=10\end{matrix}\right.\)(3)
Từ (1),(2),(3) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_B+x_C=4\\x_A+x_C=8\\x_A+x_B=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_B=4-x_C\\x_A=8-x_C\\4-x_C+8-x_C=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}12-2x_C=-6\\x_B=4-x_C\\x_A=8-x_C\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_C=9\\x_B=4-9=-5\\x_A=8-9=-1\end{matrix}\right.\)
Từ (1),(2),(3) ta có hệ phương trình:
\(\left\{{}\begin{matrix}y_B+y_C=6\\y_A+y_C=-2\\y_A+y_B=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y_B=6-y_C\\y_A=-2-y_C\\6-y_C-2-y_C=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4-2\cdot y_C=10\\y_B=6-y_C\\y_A=-2-y_C\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y_C=-3\\y_B=6+3=9\\y_A=-2+3=1\end{matrix}\right.\)
Vậy: C(9;-3); B(-5;9); A(-1;1)
Gọi (d1): ax+by+c=0 là phương trình đường thẳng AB
A(-1;1); B(-5;9)
\(\overrightarrow{AB}=\left(-4;8\right)=\left(-1;2\right)\)
=>VTPT là (2;1)
Phương trình AB là:
2[x-(-1)]+1(y-1)=0
=>2(x+1)+1(y-1)=0
=>2x+2+y-1=0
=>2x+y+1=0
Gọi (d2): ax+by+c=0 là phương trình đường thẳng AC
A(-1;1); C(9;-3)
\(\overrightarrow{AC}=\left(10;-4\right)=\left(5;-2\right)\)
=>VTPT là (2;5)
Phương trình AC là:
2(x+1)+5(y-1)=0
=>2x+2+5y-5=0
=>2x+5y-3=0
Gọi (d3): ax+by+c=0 là phương trình đường thẳng BC
B(-5;9); C(9;-3)
\(\overrightarrow{BC}=\left(14;-12\right)=\left(7;-6\right)\)
=>VTPT là (6;7)
Phương trình đường thẳng CB là:
6(x+5)+7(y-9)=0
=>6x+30+7y-63=0
=>6x+7y-33=0
\(\overrightarrow{BC}=\left(7;-6\right)\)
=>VTPT là (6;7)
mà trung điểm của BC là M(2;3)
nên Phương trình đường trung trực của BC là:
\(6\left(x-2\right)+7\left(y-3\right)=0\)
=>6x-12+7y-21=0
=>6x+7y-33=0
C(9;-3); B(-5;9); A(-1;1)
\(\overrightarrow{AC}=\left(10;-4\right)=\left(5;-2\right)\)
=>VTPT là (2;5)
Phương trình đường trung trực của AC là:
\(2\left(x-4\right)+5\left(y+1\right)=0\)
=>2x-8+5y+5=0
=>2x+5y-3=0
\(\overrightarrow{AB}=\left(-4;8\right)=\left(-1;2\right)\)
=>VTPT là (2;1)
Phương trình trung trực của AB là:
\(2\left(x+3\right)+1\left(y-5\right)=0\)
=>2x+6+y-5=0
=>2x+y+1=0
pt 3 cạnh của tam giác là pt từng cạnh à
UKM, ĐÚNG R