Lời giải:

Áp dụng BĐT AM-GM:
$M\geq 2\sqrt{\frac{1}{xy}}.\sqrt{1+x^2y^2}=2\sqrt{\frac{x^2y^2+1}{xy}}$
$=2\sqrt{xy+\frac{1}{xy}}$

Áp dụng BĐT AM-GM tiếp:

$1\geq x+y\geq 2\sqrt{xy}\Rightarrow xy\leq \frac{1}{4}$
$xy+\frac{1}{xy}=(xy+\frac{1}{16xy})+\frac{15}{16xy}$

$\geq 2\sqrt{xy.\frac{1}{16xy}}+\frac{15}{16xy}$

$\geq 2\sqrt{\frac{1}{16}}+\frac{15}{16.\frac{1}{4}}=\frac{17}{4}$

$\Rightarrow M\geq 2\sqrt{\frac{17}{4}}=\sqrt{17}$

Vậy $M_{\min}=\sqrt{17}$. Giá trị này đạt tại $x=y=\frac{1}{2}$

\(Q=\left(x+y\right)^3-3xy\left(x+y\right)+\left(x+y\right)^2-2xy\)

\(Q=8-6xy+4-2xy=12-8xy\)

\(Q=12-8x\left(2-x\right)=12-16x+8x^2=8\left(x-1\right)^2+4\ge4\)

\(Q_{min}=4\) khi \(x=y=1\)

Đang 8xy thành 8x² vậy thầy ;;-;;

\(\Rightarrow x^2+y^2\ge2\sqrt{x^2y^2}=2xy\)

\(\Rightarrow1\ge2xy\)

\(\Rightarrow\frac{1}{2}\ge xy\)

Có \(x+y\ge2\sqrt{xy}\ge2\sqrt{\frac{1}{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}\)

Vậy \(Min_{x+y}=\sqrt{2}\)

Làm tương tự với max

Thêm đk: x,y>0

Tìm max:

Áp dụng BĐT bunhiacopxki ta có:

\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x+y\right)^2\)

\(\Leftrightarrow2\ge\left(x+y\right)^2\)

\(\Leftrightarrow\sqrt{2}\ge x+y\)

Dấu " = " xảy ra <=> x=y

KL:...............................

We have : \(A=x+y+\dfrac{1}{2x}+\dfrac{2}{y}=\dfrac{x+y}{2}+\left(\dfrac{y}{2}+\dfrac{2}{y}\right)+\left(\dfrac{1}{2x}+\dfrac{x}{2}\right)\)

\(Applying\) C-S we have : \(\dfrac{y}{2}+\dfrac{2}{y}\ge2;\dfrac{1}{2x}+\dfrac{x}{2}\ge1\)

x + y \(\ge3\)  \(\Rightarrow\dfrac{x+y}{2}\ge\dfrac{3}{2}\)

So : \(A\ge\dfrac{3}{2}+2+1=\dfrac{9}{2}\)

" = " \(\Leftrightarrow x=1;y=2\)

\(x\ge2y\Rightarrow\dfrac{x}{y}\ge2\)

\(M=\dfrac{x}{y}+\dfrac{y}{x}=\dfrac{x}{4y}+\dfrac{y}{x}+\dfrac{3}{4}.\dfrac{x}{y}\ge2\sqrt{\dfrac{xy}{4xy}}+\dfrac{3}{4}.2=\dfrac{5}{2}\)

\(M_{min}=\dfrac{5}{2}\) khi \(x=2y\)

\(M=\dfrac{x}{y}+\dfrac{y}{x}=\dfrac{x}{y}+\dfrac{1}{\dfrac{x}{y}}\ge2+\dfrac{1}{2}=\dfrac{5}{2}\)

giải theo cách này có được không ạ

Vì

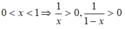
Áp dụng bất đẳng thức Cô – si đối với hai số 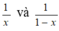 ta được:

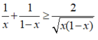
Vì 0 < x < 1 ⇒ 1 - x > 0

Áp dụng bất đẳng thức Cô – si đối với hai số 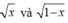 ta được:

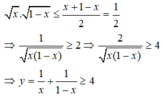
Dấu “ = ” xảy khi và chỉ khi

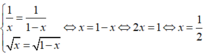
Vậy giá trị nhỏ nhất của hàm số bằng 4 tại x = 1/2