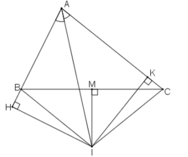
Gọi đường trung trực của BC cắt BC tại M.

Xét ΔBMI và ΔCMI, ta có:

∠(BMI) = ∠(CMI) = 90o (gt)

BM = CM ( vì M là trung điểm của BC )

MI cạnh chung

Suy ra: ΔBMI = ΔCMI(c.g.c)

Suy ra: IB = IC ( hai cạnh tương ứng)

Xét hai tam giác vuông ΔIHA và ΔIKA, ta có:

∠(HAI) = ∠(KAI) ( vì AI là tia phân giác của góc BAC).

∠(IHA) = ∠(IKA) = 90o

AI cạnh huyền chung

Suy ra: ΔIHA = ΔIKA(cạnh huyền góc nhọn)

Suy ra: IH = IK (hai cạnh tương ứng)

Xét hai tam giác vuông ΔIHB và ΔIKC, ta có:

IB = IC ( chứng minh trên )

∠(IHB) =∠(IKC) =90o

IH = IK (chứng minh trên)

Suy ra: ΔIHB = ΔIKC(cạnh huyền.cạnh góc vuông)

Suy ra: BH = CK(hai cạnh tương ứng)

ụa nếu vẫy giờ sao cm đc bh=ck

???

Xét ∆BMI và ∆CMI, ta có:

+) BM = CM (vì IM là đường trung trực của BC)

+) \(\widehat{BMI}=\widehat{CMI}=90^0\)

+) MI cạnh chung 

Suy ra: ∆BMI = ∆CMI (c.g.c)

⇒ IB = IC (hai cạnh tương ứng)

Xét hai tam giác vuông IHA và IKA, có: 

+) \(\widehat{HAI}=\widehat{KAI}\) (AI là phân giác góc A)

+) AI cạnh huyền chung

Suy ra: ∆IHA = ∆IKA (cạnh huyền - góc nhọn)

Suy ra: IH = IK (hai cạnh tương ứng)

Xét hai tam giác vuông IHB và IKC, có:

+) IB = IC (chứng minh trên)

+) IH = IK (chứng minh trên)

Suy ra: ∆IHB = ∆IKC (cạnh huyền - cạnh góc vuông)

Suy ra: BH = CK (2 cạnh tương ứng)

dcm

Gọi M là trung điểm của BC

Xét hai tam giác vuông BMI và CMI có:

BM = CM (vì M là trung điểm của BC)

MI: cạnh chung

Vậy: \(\Delta BMI=\Delta CMI\left(hcgv\right)\)

Suy ra: IB = IC (hai cạnh tương ứng)

Xét hai tam giác vuông AHI và AKI có:

AI: cạnh huyền chung

\(\widehat{HAI}=\widehat{KAI}\left(gt\right)\)

Vậy: \(\Delta AHI=\Delta AKI\left(ch-gn\right)\)

Suy ra: IH = IK (hai cạnh tương ứng)

Xét hai tam giác vuông IHB và IKC có:

IB = IC (cmt)

IH = IK (cmt)

Vậy: \(\Delta IHB=\Delta IKC\left(ch-cgv\right)\)

Suy ra: BH = CK (hai cạnh tương ứng).

*Hình ảnh chỉ mang tính chất minh hoạ, mong bn thông cảm

1.Vì các tia phân giác của các góc B và C cắt nhau tại I

\(\Rightarrow\)I là giao của các đường phân giác trong tam giác

\(\Rightarrow\)AI là tia phân giác của góc A

1.

Kẻ: \(ID\perp AB;IE\perp BC;IF\perp AC\)

\(\widehat{IDB}=\widehat{IEB}=90^0\)

\(\widehat{DBI}=\widehat{EIB}\left(gt\right)\)

BI cạnh huyền chung

⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)

Suy ra: ID = IE (hai cạnh tương ứng)       (1)

Xét hai tam giác vuông IEC và IFC, ta có ;

\(\widehat{IEC}=\widehat{IFC}=90^0\)

\(\widehat{ECI}=\widehat{FCI}\left(gt\right)\)

CI canh huyền chung

Suy ra:  ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)

Suy ra: IE = IF (hai cạnh tương ứng)           (2)

Từ (1) và (2) suy ra: ID = IF

Xét hai tam giác vuông IDA và IFA, ta có:

         \(\widehat{IDA}=\widehat{IFA}=90^0\)

            ID = IF (chứng minh trên)

            AI cạnh huyền chung

Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)

Suy ra\(\widehat{DAI}=\widehat{FAI}\) (hai góc tương ứng)

Vậy AI là tia phân giác của \(\widehat{A}\)

4578

Mấy đại ca làm ơn tick giúp em 8 cái tick em đang rất cần

5342

tick cho tui lên 120 nha