Tìm x biết:
a, (1- 52/53)+(105/106-1)+(158/159-1)=|x|/318
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NK
1
23 tháng 5 2017
1/53+-1/106+-1/159=|x|/318
6/318+-3/318+-2/318=|x|/318
1/318=|x|/318
=>|x|=1
x=1 hoặc x=-1
LL
6 tháng 12 2020
\(\left(1-\frac{52}{53}\right)+\left(\frac{105}{106}-1\right)+\left(\frac{158}{159}-1\right)=\frac{\left|x\right|}{318}\)
⇔\(\frac{1}{53}+\frac{-1}{106}+\frac{-1}{159}=\frac{\left|x\right|}{318}\)
⇔\(\frac{1}{138}=\frac{\left|x\right|}{318}\)
⇒\(\left|x\right|=1\)
⇔\(\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Vậy x∈\(\left\{-1;1\right\}\)
16 tháng 8 2023
a) Ta có A = 21 + 22 + 23 + ... + 22022
2A = 22 + 23 + 24 + ... + 22023
2A - A = ( 22 + 23 + 24 + ... + 22023 ) - ( 21 + 22 + 23 + ... + 22022 )
A = 22023 - 2
Lại có B = 5 + 52 + 53 + ... + 52022
5B = 52 + 53 + 54 + ... + 52023
5B - B = ( 52 + 53 + 54 + ... + 52023 ) - ( 5 + 52 + 53 + ... + 52022 )
4B = 52023 - 5
B = \(\dfrac{5^{2023}-5}{4}\)
b) Ta có : A + 2 = 2x
⇒ 22023 - 2 + 2 = 2x
⇒ 22023 = 2x
Vậy x = 2023
Lại có : 4B + 5 = 5x
⇒ 4 . \(\dfrac{5^{2023}-5}{4}\) + 5 = 5x
⇒ 52023 - 5 + 5 = 5x
⇒ 52023 = 5x
Vậy x = 2023
NT
3
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 12 2022
a, 159 - ( 25 - x) = 43
159 - 25 + x = 43
134 + x = 43
x = 43 - 134
x = - 91
b, ( 79 -x) - 43 = -( 17 -52)
79 - x - 43 = -( -35)
36-x = 35
x = 36- 35
x = 1
AH
Akai Haruma
Giáo viên
13 tháng 12 2022
Lời giải:
a. $(x-3)(y+1)=5=1.5=5.1=(-1)(-5)=(-5)(-1)$
Vì $x-3, y+1$ cũng là số nguyên nên ta có bảng sau:
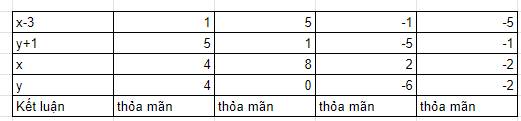
b.
$A=21+5+(5^2+5^3)+(5^4+5^5)+....+(5^{98}+5^{99})$
$=26+5^2(1+5)+5^4(1+5)+....+5^{98}(1+5)$
$=2+24+(1+5)(5^2+5^4+...+5^{98}$
$=2+24+6(5^2+5^4+....+5^{98})=2+6(4+5^2+5^4+...+5^{98})$
$\Rightarrow A$ chia $6$ dư $2$.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
30 tháng 7 2023
A= 1 + 5 + 52 + 5 3 + ... + 5800
5A= 5 + 52 + 53 + .... +5 800 + 5801
5A - A = 5801 - 1
4a = 5801 - 1
5801 - 1 +1 = 5n
⇒ 5801 = 5n ⇒ n = 801
=> \(\frac{1}{53}\)+ \(\frac{-1}{106}\)+\(\frac{-1}{159}\)= \(\frac{\left|x\right|}{318}\)
=> \(\frac{1}{318}\)= \(\frac{\left|x\right|}{318}\)
=> x thuộc {1; -1}
\(\left(1-\frac{52}{53}\right)+\left(\frac{105}{106}-1\right)+\left(\frac{158}{159}-1\right)=\frac{\left|x\right|}{318}\)
\(\Rightarrow\frac{1}{53}+\frac{-1}{106}+\frac{-1}{159}=\frac{\left|x\right|}{318}\)
\(\Rightarrow\frac{1}{318}=\frac{\left|x\right|}{318}\)
\(\Rightarrow\left|x\right|=1\)
\(\Rightarrow x=\pm1\)
Vậy..............................