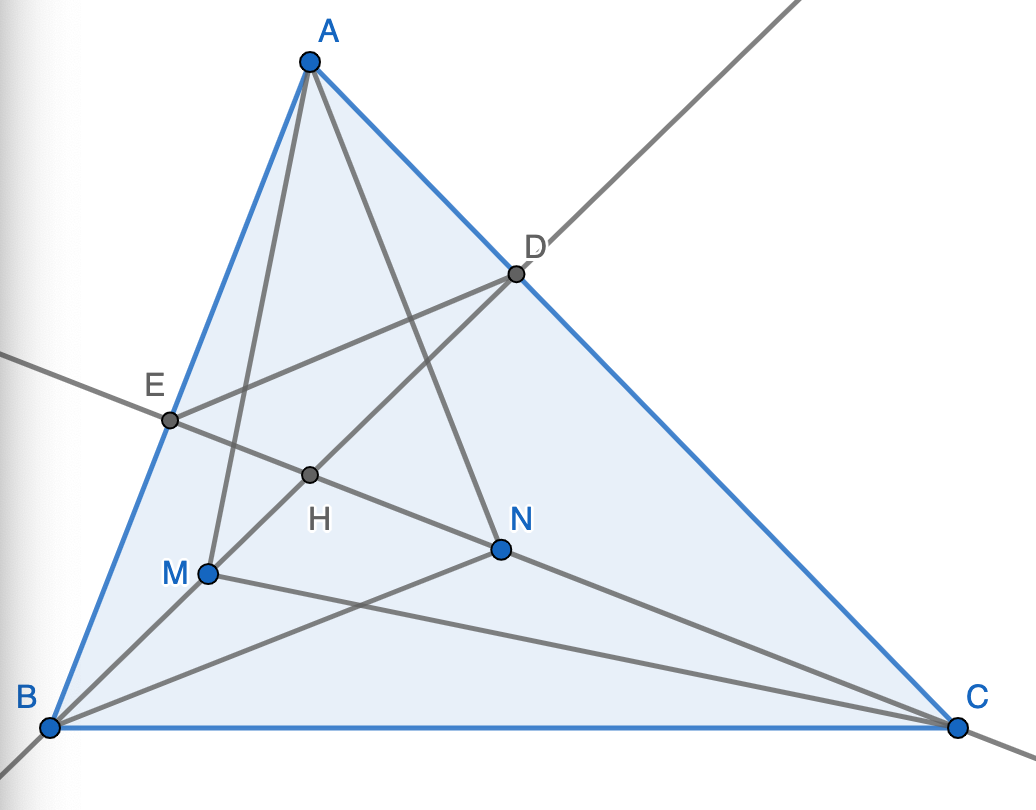
Cho tam giác ABC, \(\widehat{A}\) = 1200. Phân giác BD và CE cắt nhau tại O. Trên cạnh BC lấy hai điểm M và N sao cho \(\widehat{BOM}\) = \(\widehat{CON}\)= 300. Số đo \(\widehat{MON}\) _______
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì hai đường phân giác \(BD,CE\)cắt nhau tại \(O\)nên \(O\)là tâm đường tròn ngoại tiếp tam giác \(ABC\)
Do góc \(\widehat{BOC}\)là góc ở tâm cùng chắn cung \(\widebat{BC}\)với góc \(\widehat{BAC}\)Nên \(\widehat{BOC}=2\widehat{BAC}=120^0=120^0\)
mà \(\widehat{BOM}+\widehat{MON}+\widehat{NOC}=\widehat{BOC}\Rightarrow\widehat{MON}=\widehat{BOC}-\widehat{NOC}-\widehat{MOB}=120^0-30^0-30^0=60^0\)


a) Ta có: \(\widehat{IOK}=\widehat{BOC}-\widehat{BOI}-\widehat{KOC}=\widehat{BOC}-60^o\)
Mà \(\widehat{BOC}=180^o-\widehat{B_1}-\widehat{C_1}=180^o-\left(\frac{\widehat{B}}{2}+\frac{\widehat{C}}{2}\right)=180^o-\frac{180^o-\widehat{A}}{2}=180^o-30^o=150^o\)
\(\Rightarrow\widehat{IOK}=150^o-60^o=90^o\Rightarrow OI\perp OK\)
b) Ta có: \(\widehat{BOE}=\widehat{COD}=180^o-30^o-90^o-30^o=30^o\)
Xét \(\Delta BEO;\Delta BIO\); có:
\(\widehat{B_1}=\widehat{B_2}\left(gt\right);\) Chung BO \(;\widehat{IOB}=\widehat{EOB}=30^o\)
=> \(\Rightarrow\Delta BEO=\Delta BIO\left(g.c.g\right)\Rightarrow BE=BI.\)
Tương tự thì KC=DC
Mà BC>BI+KC => BE > BE+DC

Theo đề có: `ΔAMC` là Δ vuông, đường cao `MD`.
=> `AM^2=AD.AC` (1)
`ΔANB` là Δ vuông, đường cao `NE`:
=> `AN^2=AE.AB` (2)
Lại có: `ΔABD=ΔACE`(g.g)
=> \(\dfrac{AB}{AC}=\dfrac{AD}{AE}\Leftrightarrow AB.AE=AC.AD\left(3\right)\)
Từ (1), (2), (3) suy ra: `AM=AD` (đpcm)
$HaNa$

a) Ta có \(\widehat{B}+\widehat{C}=90^o\) mà \(\widehat{B_1}=\widehat{B_2}=\frac{\widehat{B}}{2};\widehat{C_1}=\widehat{C_2}=\frac{\widehat{C}}{2}\) nên \(\widehat{B_2}+\widehat{C_2}=\frac{\widehat{B}+\widehat{C}}{2}=\frac{90^o}{2}=45^o\)
Xét tam giác BOC, có \(\widehat{BOC}+\widehat{B_2}+\widehat{C_2}=180^o\Rightarrow\widehat{BOC}=180^o-45^o=135^o\)
b) Xét tam giác BAD và BMD có:
Cạnh BD chung
\(\widehat{B_1}=\widehat{B_2}\)
AB = MB (gt)
\(\Rightarrow\Delta BAD=\Delta BMD\left(c-g-c\right)\)
\(\Rightarrow\widehat{BMD}=\widehat{BAD}=90^o\)
Hoàn toàn tương tự \(\Delta EAC=\Delta ENC\left(c-g-c\right)\Rightarrow\widehat{ENC}=\widehat{EAC}=90^o\)
Ta có EN và DM cùng vuông góc với BC nên EN // DM
c) Theo câu b, \(\Delta BAD=\Delta BMD\Rightarrow AD=MD;\widehat{BDA}=\widehat{BDM}\)
Từ đó ta có \(\Delta OAD=\Delta OMD\left(c-g-c\right)\Rightarrow OA=OM.\)
Tương tự : \(\Delta OAE=\Delta ONE\left(c-g-c\right)\Rightarrow OA=ON.\)
Vậy nên OA = OM = ON
d) Ta có \(\Delta OAD=\Delta OMD\left(c-g-c\right)\Rightarrow\widehat{OAD}=\widehat{OMD}\)
\(\Delta OAE=\Delta ONE\left(c-g-c\right)\Rightarrow\widehat{OAE}=\widehat{ONE}\)
\(\Rightarrow\widehat{ONE}+\widehat{OMD}=\widehat{OAE}+\widehat{OAD}=\widehat{EAD}=90^o\)
\(\Rightarrow\widehat{NOM}=90^o\) (Dạng bài qua O kẻ đường thẳng song song với EN và DM)
Vậy tam giác OMN vuông cân hay \(\widehat{ONM}+\widehat{OMN}=90^o\)
Xét tam giác AMN có \(\widehat{MAN}+\widehat{ANM}+\widehat{AMN}=180^o\)
\(\Leftrightarrow\widehat{MAN}+\widehat{ANO}+\widehat{ONM}+\widehat{AMO}+\widehat{OMN}=180^o\)
\(\Leftrightarrow\widehat{MAN}+\widehat{NAO}+\widehat{MAO}=180^o-90^o=90^o\)
\(\Leftrightarrow\widehat{2MAN}=90^o\)
\(\Leftrightarrow\widehat{MAN}=45^o\)

Bổ sug đề: Cho (O), BD,CE là các dây của (O)
Sửa đề: Chứng minh góc BOE=góc EDB+góc ECB
1/2(góc EDB+góc ECB)
=1/2(1/2sđ cung EB+1/2sđ cung EB)
=1/2sđ cung EB
=1/2*góc BOE
=>góc EDB+góc ECB=góc BOE

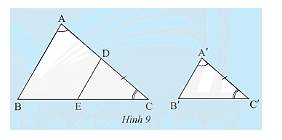
a) Vì \(ED//AB \Rightarrow \Delta DEC\backsim\Delta ABC\) (định lí)
b) Vì \(ED//AB \Rightarrow \widehat {CDE} = \widehat {CAB}\) (hai góc đồng vị)
Mà \(\widehat {CAB} = \widehat {A'}\). Do đó, \(\widehat {CDE} = \widehat {B'A'C'}\).
Xét tam giác \(A'B'C'\) và tam giác \(DEC\) ta có:
\(\widehat {B'A'C'} = \widehat {CDE}\) (chứng minh trên)
\(A'C' = CD\) (giải thuyết)
\(\widehat {C'} = \widehat C\) (giả thuyết)
Do đó, \(\Delta A'B'C' = \Delta DEC\) (g.c.g)
c) Vì tam giác \(\Delta A'B'C'\backsim\Delta DEC\) (tính chất)
Mà \(\Delta DEC\backsim\Delta ABC\) nên \(\Delta ABC\backsim\Delta A'B'C'\).

t/g ABC có ABC +ACB=180-120=60
2CBD+2ECB=60
CBD+ECB=60:2=30
Xét t/g OBC có:BOC+CBD+ECB=180
BOC =180-30
BOC =150
MÀ BOM+CON+MON=160
NÊN MON =150-30-30
MON =90
thanks