Câu 5:Biết rằng
Số trong đẳng thức trên bằng .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BF
1
12 tháng 8 2019
Ta có :
\(\frac{12}{-20}=\frac{3}{-5}\) ; \(\frac{12}{3}=-\frac{20}{-5}\)
\(-\frac{5}{-20}=\frac{3}{12}\); \(-\frac{5}{3}=-\frac{20}{12}\)
Chúc bạn học tốt !!!
LA
22 tháng 6 2017
Giải
\(\frac{2}{8}+\frac{2}{3}=\frac{12}{48}+\frac{32}{48}=\frac{44}{48}=\frac{11}{12}\)
Vậy....
CM
12 tháng 12 2018
Đáp án A.
Vì y = f x là hàm số đồng biến trên 1 ; 4 ⇒ f x ≥ f 1 = 3 2 .
Khi đó:
x + 2 x . f x = f ' x 2 ⇔ x . 2 f x + 1 = f ' x ⇔ f ' x 2 f x + 1 = x ( * ) .
Lấy nguyên hàm 2 vế của (*), ta được:
∫ f ' x 2 f x + 1 d x = ∫ x d x = 2 3 x x + C ( 1 ) .
Đặt t = 2 f x + 1
⇔ d t = f ' x 2 f x + 1 d x ⇒ ∫ f ' x 2 f x + 1 d x = ∫ d t = t ( 2 ) .
Từ (1), (2) suy ra 2 f x + 1 = 2 3 x x + C mà f 1 = 2 3 ⇒ 2. 3 2 + 1 = C + 2 3 ⇔ C = 4 3 .
Do đó:
2 f x + 1 = 2 3 x x + 4 3 ⇔ f x = 1 2 2 3 x x + 4 3 2 − 1 .
Vậy ∫ 1 4 f x d x = 1186 45 .
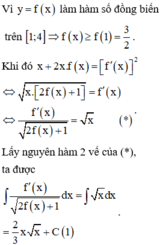
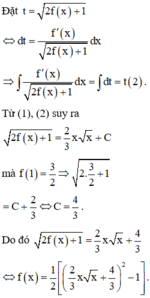
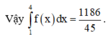
\(\frac{1}{x\left(x+1\right)}+\frac{1}{\left(x+1\right)\left(x+2\right)}+\frac{1}{\left(x+2\right)\left(x+3\right)}+...+\frac{1}{\left(x+99\right)\left(x+100\right)}=\frac{k}{x\left(x+100\right)}\)
\(\frac{1}{x}-\frac{1}{x+1}+\frac{1}{x+1}-\frac{1}{x+2}+\frac{1}{x+2}-\frac{1}{x+3}+...+\frac{1}{x+99}-\frac{1}{x+100}=\frac{k}{x\left(x+100\right)}\)
\(\frac{1}{x}-\frac{1}{x+100}=\frac{k}{x\left(x+100\right)}\)
\(\frac{x+100}{x\left(x+100\right)}-\frac{x}{x\left(x+100\right)}=\frac{k}{x\left(x+100\right)}\)
k = 100
k=100