Trên mặt phẳng tọa độ Oxy cho 4 điểm \(A\left(7;-3\right);B\left(8;4\right);C\left(1;5\right);D\left(0;-2\right)\). Chứng minh rằng tứ giác ABCD là hình vuông ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(1); vecto u=2*vecto a-vecto b
=>\(\left\{{}\begin{matrix}x=2\cdot1-0=2\\y=2\cdot\left(-4\right)-2=-10\end{matrix}\right.\)
(2): vecto u=-2*vecto a+vecto b
=>\(\left\{{}\begin{matrix}x=-2\cdot\left(-7\right)+4=18\\y=-2\cdot3+1=-5\end{matrix}\right.\)
(3): vecto a=2*vecto u-5*vecto v
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\cdot\left(-5\right)-5\cdot0=-10\\b=2\cdot4-5\cdot\left(-3\right)=15+8=23\end{matrix}\right.\)
(4): vecto OM=(x;y)
2 vecto OA-5 vecto OB=(-18;37)
=>x=-18; y=37
=>x+y=19

Phương trình của đường thẳng AB có dạng: y = ax + b.
Do phương trình đi qua A(4;5) và B(1; -1) nên ta có:
5 = a.4 + b (1)
-1 = a.1 + b (2)
Trừ từng vế của (1) và (2), ta có: 6 = 3a ⇒ a = 2.
Thay a = 2 và (1) để tìm b, ta có 5 = 2.4 + b ⇒ b = -3.
Vậy phương trình đường thẳng AB là: y = 2x – 3.
Làm tương tự như trên, ta có:
Phương trình đường thẳng BC là: y = -x.
Phương trình đường thẳng CD là: y = x – 8.
Phương trình đường thẳng DA là: y = -2x + 13.

Hai đường chéo AC và BD vuông góc với nhau tại I.
- Đường thẳng AB có hệ số góc bằng 2, do đó ta có
tgα = 2 ⇒ α = 63 ° 26 ' (tính trên máy tính bỏ túi).
Suy ra ∠ (ABD) ≈ 63 ° 26 '
Tam giác ABD cân, nên cũng có ∠ (ADB) ≈ 63 ° 26 '
Từ đó suy ra ∠ (BAD) = 180 ° - 2. 63 ° 26 ' ≈ 53 ° 8 '

\(a,\) Thay \(x=3;y=4\Rightarrow\dfrac{4}{3}\cdot3=4\) (đúng)
Vậy \(A\left(3;4\right)\in y=\dfrac{4}{3}x\)

a)
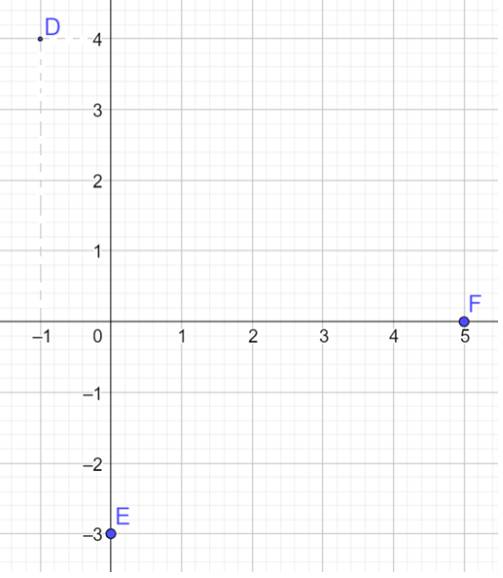
b) Vì tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ của điểm M (với mọi M) nên ta có:
\(\overrightarrow {OD} = \left( { - 1;4} \right),\overrightarrow {OE} = \left( {0; - 3} \right),\overrightarrow {OF} = \left( {5;0} \right)\)
c)
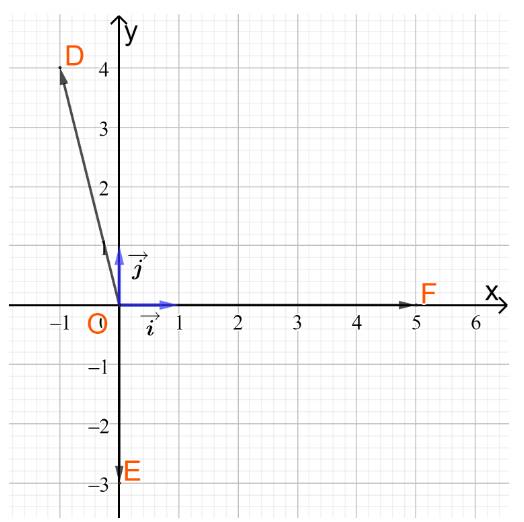
Từ hình vẽ ta có tọa độ của hai vectơ và \(\overrightarrow j \)là
và \(\overrightarrow j = (0;1)\)

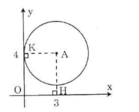
Kẻ AH ⊥ Ox, AK ⊥ Oy.
Vì AH = 4 > R = 3 nên đường tròn tâm (A) và trục hoành không giao nhau.
Vì AK = 3 = R nên đường tròn (A) và trục tung tiếp xúc nhau.

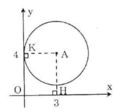
Kẻ AH ⊥ Ox, AK ⊥ Oy.
Vì AH = 4 > R = 3 nên đường tròn tâm (A) và trục hoành không giao nhau.
Vì AK = 3 = R nên đường tròn (A) và trục tung tiếp xúc nhau.
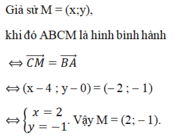
Ta có: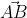 = (1; 7);
= (1; 7); 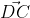 = (1; 7)
= (1; 7)
ta lại có : AB2 = 50 => AB = 5 √2
AD2 = 50 => AD = 5 √2
AB = AD, kết hợp với (1) => ABCD là hình thoi (2)
Mặt khác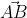 = (1; 7);
= (1; 7); 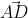 = (-7; 1)
= (-7; 1)
1.7 + (-7).1 = 0 =>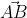 ⊥
⊥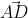 (3)
(3)
Kết hợp (2) và (3) suy ra ABCD là hình vuông