a) Ta có đồ thị hàm số y = ax2 đi qua điểm (-2 ; 2)

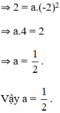
b) Tại x = -3 ta có: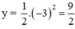 

Vậy điểm có hoành độ x = -3 thì tung độ bằng 4,5.

c) Hoành độ các điểm có tung độ y =8 thỏa mãn phương trình: 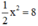 ⇔ x2 = 16 ⇔ x = 4 hoặc x = -4.

Vậy các điểm thuộc parabol có tung độ bằng 8 là (4; 8) và (-4; 8).

Tại x = -3 ta có: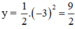 

Vậy điểm có hoành độ x = -3 thì tung độ bằng 4,5.

Hoành độ các điểm có tung độ y =8 thỏa mãn phương trình: 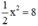 ⇔ x2 = 16 ⇔ x = 4 hoặc x = -4.

Vậy các điểm thuộc parabol có tung độ bằng 8 là (4; 8) và (-4; 8).

Đáp án D

Số nguyên dương nhỏ nhất là 1.

Do đó, tung độ của điểm thuộc parabol có hoành độ 1 là: y = 3. 1 2  = 3

Lời giải:

Theo bài ra thì tọa độ đỉnh của parabol là $(-2,19)$

Từ hàm $y=ax^2+bx+3=a(x+\frac{b}{2a})^2+3-\frac{b^2}{4a}$ ta có tọa độ đỉnh của parabol là:
$(\frac{-b}{2a}, 3-\frac{b^2}{4a})$

$\Rightarrow \frac{-b}{2a}=-2; 3-\frac{b^2}{4a}=19$

$\Rightarrow a=-4; b=-16$

+ Giao điểm của parabol với trục tung:

Tại x = 0 thì y = a.02 + b.0 + c = c.

Vậy giao điểm của parabol với trục tung là A(0 ; c).

+ Giao điểm của parabol với trục hoành :

Tại y = 0 thì ax2 + bx + c = 0 (*).

Để parabol cắt trục hoành tại hai điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt ⇔ Δ = b2 – 4ac > 0.

Khi Δ > 0 thì phương trình (*) có hai nghiệm là

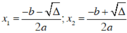
Tọa độ hai giao điểm là

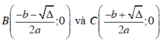
Thay y = 4 vào phương trình đường thẳng d ta được 2x + 2 = 4 ⇔ x = 1

Nên tọa độ giao điểm của đường thẳng d và parabol (P) là (1; 4)

Thay x = 1; y = 4 vào hàm số y = 1 − 2 m 2 x 2 ta được:

1 − 2 m 2 .1 2 = 4 ⇔ 1 – 2m = 8 ⇔ m = − 7 2

Xét phương trình hoành độ giao điểm của d và (P):

4x² = 2x + 2 ⇔ 2x² – x – 1 = 0

⇔ (2x + 1) (x – 1) = 0

⇔ x = 1 x = − 1 2

Vậy hoành độ giao điểm còn lại là

Đáp án cần chọn là: A