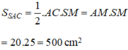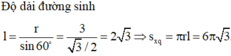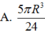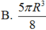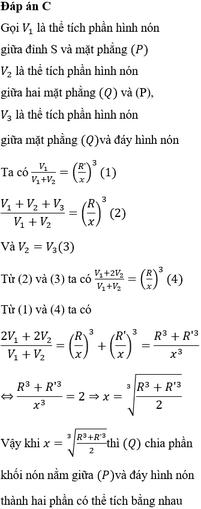Cho khối nón có bán kính đáy r = 12cm và có góc ở đỉnh là \(\alpha=120^0\). Hãy tính diện tích của thiết diện đi qua hai đường sinh vuông góc với nhau ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



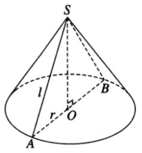
Theo giả thiết ta có góc ở đỉnh của hình nón là ∠ ASB = α = 120 ° . Gọi O là tâm của đường tròn đáy. Ta có: ∠ ASO = 60 °
và 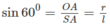
với l là độ dài đường sinh của hình nón.
Vậy
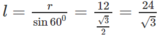
Khi có hai đường sinh vuông góc với nhau ta có tam giác vuông có diện tích là l 2 /2. Do đó, diện tích của thiết diện là:
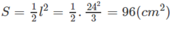

Đáp án D
Phương pháp giải: Xác định độ dài đường sinh qua góc và bán kính, tính diện tích tam giác vuông bằng tích hai cạnh góc vuông
Lời giải: Ta có 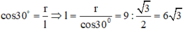
Diện tích cần tính là 

Gọi hình nón đã cho có đỉnh là S và H là tâm đường tròn đáy.
Thiết diện đi qua đỉnh S là tam giác SAC (với A và C thuộc đường tròn đáy)
Gọi M là trung điểm của AC.
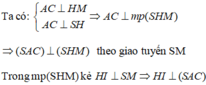
Do đó, d( H; (SAC))= HI = 12
Trong tam giác vuông SHM ta có:
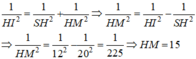
Trong tam giác vuông HAM ta có:
AM2 = HA2 – HM2 = 252 – 152 = 400 nên AM = 20 (cm)
Ta có:
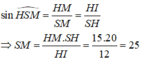
Do đó, diện tích thiết diện SAC là: