|
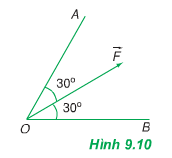
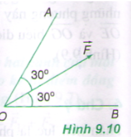
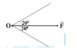
Phân tích lực \(\overrightarrow{F}\) thành hai lực \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) theo hai phương OA và OB (hình 9.10). Giá trị nào sau đây là độ lớn của hai lực thành phần? A. F1 = F2 = F; B. F1 = F2 = \(\dfrac{1}{2}\)F; C. F1 = F2 = 1,15F; D. F1 = F2 = 0,58F. |
 |
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
a)
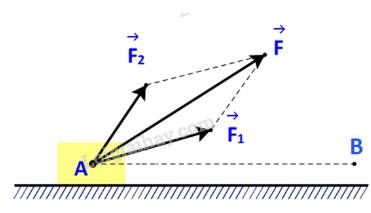
Gọi \(A,{A_1},{A_2}\) lần lượt là công sinh bởi lực \(\overrightarrow F \), \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).
Ta cần chứng minh: \(A = {A_1} + {A_2}\)
Xét lực \(\overrightarrow F \), công sinh bởi lực \(\overrightarrow F \) là: \(A = \left| {\overrightarrow F } \right|.{\rm{ AB}}.\cos \left( {\overrightarrow F ,\overrightarrow {AB} } \right) = \overrightarrow F .\overrightarrow {AB} \)
Tương tự, ta có: \({A_1} = \overrightarrow {{F_1}} .\overrightarrow {AB} \), \({A_2} = \overrightarrow {{F_2}} .\overrightarrow {AB} \)
Áp dụng tính chất của tích vô hướng ta có:
\({A_1} + {A_2} = \overrightarrow {{F_1}} .\overrightarrow {AB} + \overrightarrow {{F_2}} .\overrightarrow {AB} = \left( {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right).\overrightarrow {AB} = \overrightarrow F .\overrightarrow {AB} = A\)
b)
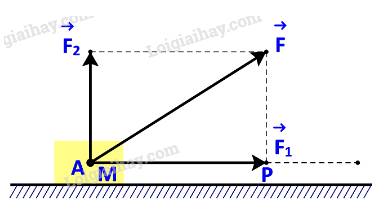
Vì \(\overrightarrow {{F_2}} \)tương ứng vuông góc với phương chuyển động nên \(\overrightarrow {{F_2}} \bot \overrightarrow {AB} \)
Do đó: công sinh bởi lực \(\overrightarrow {{F_2}} \) là: \({A_2} = \overrightarrow {{F_2}} .\overrightarrow {AB} = 0\)
Mà \(A = {A_1} + {A_2}\)
\( \Rightarrow A = {A_1}\)
Vậy công sinh bởi lực \(\overrightarrow F \) bằng công sinh bởi lực \(\overrightarrow {{F_1}} \).

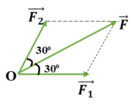
Áp dụng quy tắc hình bình hành: Từ điểm ngọn của vecto F lần lượt vẽ các đoạn song song với hai phương OA và OB ta được các vecto F1 trên OA và F2 trên OB sao cho
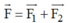
Hình bình hành có đường chéo cũng là đường phân giác của 1 góc nên nó là hình thoi.
Suy ra: F1 = F2
Mà
![]()
![]()

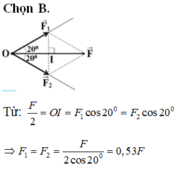
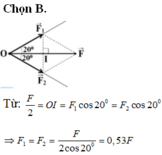
Chọn B.
Từ: F/2 = OI = F1cos200 = F2cos200
⇒ F 1 = F 2 = F 2 cos 20 0 = 0 , 53 F .
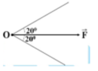


Áp dụng quy tắc hình bình hành ta có: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} \);
\(AC = OB = 600\); \(\widehat {AOB} = 60^\circ \Rightarrow \widehat {OAC} = 120^\circ \) (hai góc bù nhau trong hình bình hành).
Áp dụng định lý cos ta có:
\(OC = \sqrt {O{A^2} + A{C^2} - 2OA.AC.\cos (120^\circ )} \)
\( = \sqrt {{{400}^2} + {{600}^2} - 2.400.600.\cos (120^\circ )} \simeq 871,78\)N
Vậy độ lớn của vectơ hợp lực \(\overrightarrow F \) gần bằng 871,78 N.

Tham khảo:
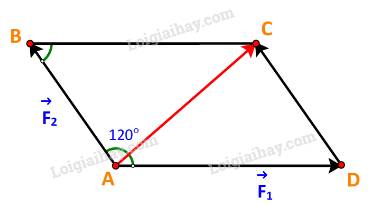
Dựng hình bình hành ABCD với hai cạnh là hai vectơ \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) như hình vẽ
Ta có:
\(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {AD} + \overrightarrow {AB} = \overrightarrow {AC} \Rightarrow \left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {AC} } \right| = AC\)
Xét \(\Delta ABC\) ta có:
\(BC = AD = \left| {\overrightarrow {{F_1}} } \right| = 3\;,AB = \;\left| {\overrightarrow {{F_2}} } \right| = 2\;.\)
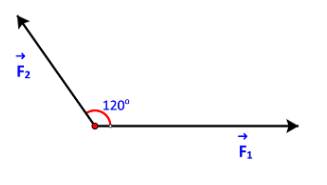
\(\widehat {ABC} = {180^o} - \widehat {BAD} = {180^o} - {120^o} = {60^o}\)
Theo định lí cosin ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos \widehat {ABC}\\ \Leftrightarrow A{C^2} = {2^2} + {3^2} - 2.2.3.\cos {60^o}\\ \Leftrightarrow A{C^2} = 7\\ \Leftrightarrow AC = \sqrt {7} \end{array}\)
Vậy \(\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \sqrt {7} \)

-Tàu sẽ chuyển động theo hướng tổng hợp lực \(\overrightarrow{F}\).
-Để tính được độ lớn của lực kéo tác dụng lên tàu ta cần xác định lực \(F_1,F_2\) và góc tạo bởi hai lực đó.


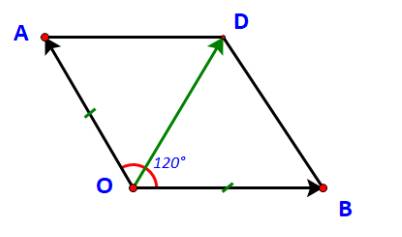
Gọi D là đỉnh thứ tư của hình bình hành OADB.
Khi đó ta có: \(\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OD} \)
Ta có: OA = OB = 120 suy ra tứ giác OADB là hình thoi
\( \Rightarrow \widehat {AOD} = \widehat {BOD} = \frac{{{{120}^o}}}{2} = {60^o}\)
\( \Rightarrow \Delta AOD\) đều (do OA = AD và \(\widehat {AOD} = {60^o}\))
\( \Rightarrow OD = OA = 120\)
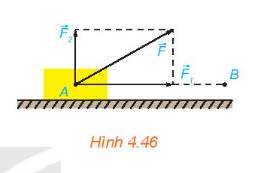
Mặt khác: Do vật đứng yên nên \(\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} + \;\overrightarrow {{F_3}} = \overrightarrow 0 \Leftrightarrow \;\overrightarrow {{F_3}} = - (\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} ) = - \overrightarrow {OD} \)
Suy ra vecto \(\overrightarrow {OC} \) là vecto đối của vecto \(\overrightarrow {OD} \)
Lại có: \(\widehat {COA} = {180^o} - \widehat {AOD} = {120^o}\).Tương tự: \(\widehat {COB} = {120^o}\)

Vậy cường độ của lực \(\overrightarrow {{F_3}} \)là 120 N, tạo với lực\(\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}} \) góc \({120^o}\).

Nếu F1=F2
do góc giữa vecto F1, F2=60o
áp dụng định lý hàm cos
F2=F12+ F22+2F1F2cos (vecto)
=> F1=0,58F
Phân tích lực F→F→ thành hai lực F1−→F1→ và F2−→F2→ theo hai phương OA và OB (hình 9.10).
Giá trị nào sau đây là độ lớn của hai lực thành phần?
A. F1 = F2 = F;
B. F1 = F2 = 1212F;
C. F1 = F2 = 1,15F;
D. F1 = F2 = 0,58F.
Nếu F1 = F2
do góc giữa vécto F1,F2 = 600
áp dụng định lý hàm cos
F2 = F12 + F22 + 2F1F2cos (vecto)F1,F2
=> F1 = 0,58F
Chọn D