Trong hình 44, hệ thức nào trong các hệ thức sau là đúng ?
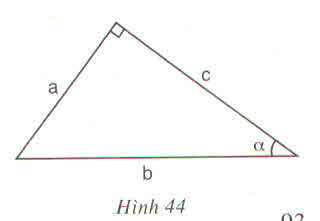
(A) \(\sin\alpha=\dfrac{b}{c}\) (B) \(cotg\alpha=\dfrac{b}{c}\) (C) \(tg\alpha=\dfrac{a}{c}\) (D) \(cotg\alpha=\dfrac{a}{c}\)
b) Trong hình 45, hệ thức nào trong các hệ thức sau không đúng ?
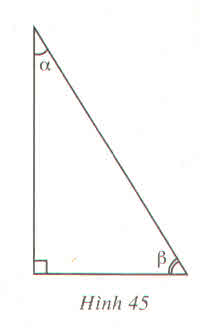
(A) \(\sin^2\alpha+\cos^2\alpha=1\)
(B) \(\sin\alpha=\cos\beta\)
(C) \(\cos\beta=\sin\left(90^0-\alpha\right)\)
(D) \(tg\alpha=\dfrac{\sin\alpha}{\cos\alpha}\)



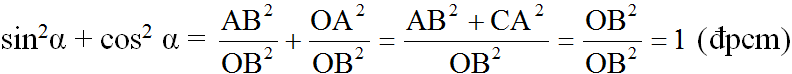
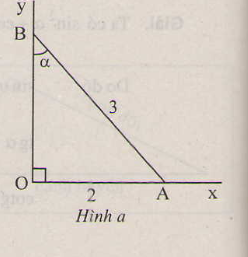
Lời giải: