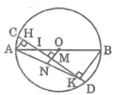
Kẻ OM ⊥ CD cắt AD tại N

Ta có: MC = MD (đường kính dây cung)

Hay MH + CH = MK + KD     (1)

Ta có: OM // BK (cùng vuông góc với CD)

Hay: MN // BK

Mà: OA = OB (= R)

Suy ra: NA = NK (tính chất đường trung bình của tam giác)

Lại có: OM // AH (cùng vuông góc với CD)

Hay: MN // AH

Mà: NA = NK (chứng minh trên)

Suy ra: MH = MK (tính chất đường trung bình của tam giác)    (2)

Từ (1) và (2) suy ra: CH = DK

Kẻ OM ⊥ CD.

Vì AH // BK (cùng vuông góc HK) nên tứ giác AHKB là hình thang.

Hình thang AHKB có:

    AO = OB (bán kính).

    OM // AH // BK (cùng vuông góc HK)

=> OM là đường trung bình của hình thang.

=> MH = MK         (1)

Vì OM ⊥ CD nên MC = MD     (2)

Từ (1) và (2) suy ra CH = DK. (đpcm)

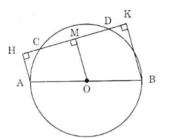
Kẻ OM ⊥ CD.

Vì AH // BK (cùng vuông góc HK) nên tứ giác AHKB là hình thang.

Hình thang AHKB có:

    AO = OB (bán kính).

    OM // AH // BK (cùng vuông góc HK)

=> OM là đường trung bình của hình thang.

=> MH = MK         (1)

Vì OM ⊥ CD nên MC = MD     (2)

Từ (1) và (2) suy ra CH = DK. (đpcm)

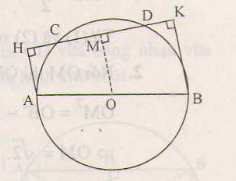
Vẽ $OM\perp CD$ ta được CM=DM. (1)

Ta có OM // AH //BK (cùng vuông góc với CD).

Mặt khác , OA=OB nên MH=MK. (2)

Từ (1) và (2) suy ra CH=DK.

Nhận xét. Kết quả của bài toán trên không thay đổi nếu ta đổi chỗ hai điểm C và D cho nhau.

VẽOM⊥CDta được CM=DM. (1)

Ta có OM // AH //BK (cùng vuông góc với CD).

Mặt khác , OA=OB nên MH=MK. (2)

Từ (1) và (2) suy ra CH=DK.

Nhận xét. Kết quả của bài toán trên không thay đổi nếu ta đổi chỗ hai điểm C và D cho nhau.

Lời giải chi tiết

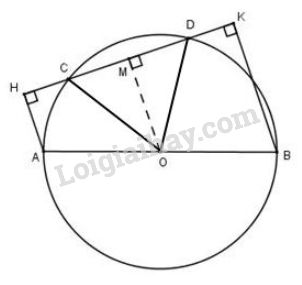
Vẽ OM⊥CDOM⊥CD 

Vì OM là một phần đường kính và CD là dây của đường tròn nên ta có M là trung điểm CD hay MC=MDMC=MD   (1) (định lý)

Tứ giác AHKBAHKB có AH⊥HK; BK⊥HK⇒HA//BKAH⊥HK; BK⊥HK⇒HA//BK.

Suy ra tứ giác AHKBAHKB là hình thang.  

Xét hình thang AHKBAHKB, ta có:

OM//AH//BKOM//AH//BK (cùng vuông góc với CDCD)

mà AO=BO=AB2AO=BO=AB2

⇒MO⇒MO là đường trung bình của hình thang AHKBAHKB.

⇒MH=MK⇒MH=MK   (2)

Từ (1) và (2)  ⇒MH−MC=MK−MD⇔CH=DK⇒MH−MC=MK−MD⇔CH=DK (đpcm)

Nhận xét: Kết quả của bài toán trên không thay đổi nếu ta đổi chỗ hai điểm CC và DD cho nhau.

Kẻ $OM$ vuông góc với dây $CD$.

Hình thang $AHKB$ có

$AO=OB$ và $OM//AH//BK$

nên $MH=MK$                                                    (1)

$OM$ vuông góc với dây $CD$ nên

$MC=MD$                                                              (2)
Từ (1) và (2) suy ra $CH=DK$.

 gọi O là tâm đường tròn đường kính AB 

Kẻ OE vuông góc vs CD (E thuộc CD)

 suy ra E là trung điểm của CD 

Mà OE là đường trung bình của hình thang ABKH (đi qua trung điểm một cạnh bên và song song vs cạnh đáy)

suy ra EH=EK mà EC=ED Suy ra đpcm