Biết rằng \(Q=\dfrac{x^2-6x+9}{x^2-9}=\dfrac{\left(x-3\right)^2}{\left(x-3\right)\left(x+3\right)}=\dfrac{x-3}{x+3}\)
Hãy tính giá trị của biểu thức Q. Câu trả lời nào sau đây sai ?
(A) Giá trị của Q tại \(x=4\) là \(\dfrac{4-3}{4+3}=\dfrac{1}{7}\)
(B) Giá trị của Q tại \(x=1\) là \(\dfrac{1-3}{1+3}=-\dfrac{1}{2}\)
(C) Giá trị của Q tại \(x=3\) là \(\dfrac{3-3}{3+3}=0\)
(D) Giá trị của Q tại \(x=3\) không xác định


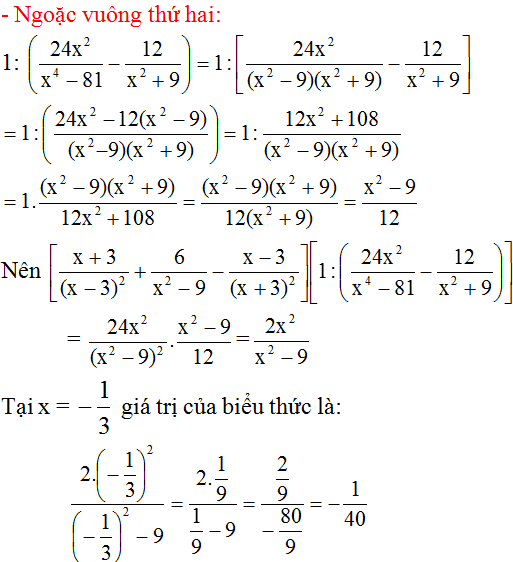




Câu trả lời sai là:
(C) Giá trị của Q tại \(x=3\) là \(\dfrac{3-3}{3+3}=0\)
Do ĐKXĐ của phương trình
\(Q=\dfrac{x^2-6x+9}{x^2-9}\) là \(x\ne\pm3\)