vẽ đường tròn ngoại tiếp ngũ giác đều ABCDE

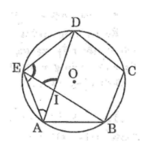
Suy ra tam giác DEI cân tại D ⇒ DI = DE

Mà DE =AE

Nên DI = AE (7)

Từ (4) và (7) suy ra:  D I 2 = AI.AD

cj kham khảo

a) Nối AC; AD

Ngũ giác ABCDE được chia thành 3 tam giác: ΔABC, ΔACD, ΔADE. Tổng các góc trong của mỗi tam giác bằng 180⁰

Tổng các góc trong của ngũ giác ABCDE là 180⁰. 3 = 540⁰

b) Vì ABCDE là ngũ giác đều nên

\(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=\widehat{E}=\frac{540^0}{5}=108^0\)

Mặt khác ΔABC cân tại B nên 

\(\widehat{BAC}+\widehat{BCA}=\frac{180^0-108^0}{2}=36^0\)

\(\Rightarrow\widehat{CAE}=\widehat{ACD}=108^0-36^0=72^0\)

\(\Rightarrow\widehat{EDC}+\widehat{ADC}=108^0+72^2=180^0\)

Suy ra ED // AC hay ED // CF.

Chứng minh tương tự ta có EF // CD

Mặt khác ED = DC (gt)

nên tứ giác CEFD là hình thoi.

Số đo mỗi góc của ngũ giác đều là 108⁰.

Ta có tam giác ABC cân tại B

⇒ A 1 ^ = C 1 ^ = ( 180 0 − 108 0 ) : 2 = 36 0 ⇒ E A C ^ = D C A ^     (1)

Chứng minh tương tự ta được:

C 3 ^ = E ^ 1 = 36 0 ⇒ C 2 ^ = 36 0  

Có C 2 ^ = E 1 ^ = 36 0 ⇒ E D / / A C       (2)

Từ (1) và (2), suy ra ACDE là hình thang cân (ĐPCM)

(Các khác: Có thể chứng minh hình thang ACDE có hai đường chéo bằng nhau)

* Chứng minh tương tự ta có J E F ^ = E F G ^ = F G H ^ = G H I ^ = H I J ^ = I J E ^ .

Vậy tứ giác CDEK là hình bình hành

mà CD = DE, suy ra hình bình hành CDEK là hình thoi (ĐPCM)

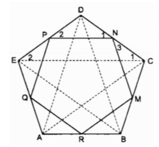
Xét △ ABC và  △  BCD:

AB = BC (gt)

∠ B = ∠ C (gt)

BC = CD (gt)

Do đó:  △  ABC =  △  BCD (c.g.c)

⇒ AC = BD (1)

Xét  △  BCD và  △  CDE:

BC = CD (gt)

∠ C =  ∠ D (gt)

CD = DE (gt)

Do đó:  △  BCD =  △  CDE (c.g.c) ⇒ BD = CE (2)

Xét  △ CDE và  △  DEA:

CD = DE (gt)

∠ D =  ∠ E (gt)

DE = EA (gt)

Do đó:  △  CDE =  △  DEA (c.g.c) ⇒ CE = DA (3)

Xét △  DEA và  △  EAB:

DE = EA (gt)

∠ E =  ∠ A (gt)

EA = AB (gt)

Do đó:  △  DEA =  △  EAB (c.g.c) ⇒ DA = EB (4)

Từ (1), (2), (3), (4) suy ra: AC = BD = CE = DA = EB

Trong  △  ABC ta có RM là đường trung bình

⇒ RM = 1/2 AC (tính chất đường trung bình của tam giác)

Mặt khác, ta có: Trong Δ BCD ta có MN là đường trung bình

⇒ MN = 1/2 BD (tính chất đường trung bình của tam giác)

Trong  △  CDE ta có NP là đường trung bình

⇒ NP = 1/2 CE (tính chất đường trung bình của tam giác)

Trong  △  DEA ta có PQ là đường trung bình

⇒ PQ = 1/2 DA (tính chất đường trung bình của tam giác)

Trong  △  EAB ta có QR là đường trung bình

⇒ QR = 1/2 EB (tính chất đường trung bình của tam giác)

Suy ra: MN = NP = PQ = QR = RM

Ta có:  ∠ A =  ∠ B =  ∠ C =  ∠ D =  ∠ E = ((5-2 ). 180 0 )/5 =  108 0

△  DPN cân tại D

⇒ ∠ (DPN) =  ∠ (DNP) = ( 180 0 -  ∠ D )/2 = ( 180 0  -  108 0 )/2 =  36 0

△  CNM cân tại C

⇒  ∠ (CNM) =  ∠ (CMN) = ( 180 0 -  ∠ D )/2 = ( 180 0  -  108 0 )/2 =  36 0

∠ (ADN) +  ∠ (PNM) +  ∠ (CNM) =  180 0

⇒  ∠ (PNM) =  180 0  - ( ∠ (ADN) +  ∠ (CNM) )

            = 180 0  - ( 36 0  –  36 0 ) =  108 0

△  BMR cân tại B

⇒  ∠ (BMR) =  ∠ (BRM) = ( 180 0 -  ∠ B )/2 = ( 180 0  -  108 0 )/2 =  36 0

∠ (CMN) +  ∠ (BRM) +  ∠ (BMR) =  180 0

⇒  ∠ (NMR) =  180 0  - ( ∠ (CMN) +  ∠ (BMR) )

            =  180 0  - ( 36 0  –  36 0 ) =  108 0

△  ARQ cân tại A

⇒  ∠ (ARQ) =  ∠ (AQR) = ( 180 0 -  ∠ A )/2 = ( 180 0  -  108 0 )/2 =  36 0

∠ (BRM) +  ∠ (MRQ) +  ∠ (ARQ) =  180 0

⇒  ∠ (MRQ) =  180 0  - ( ∠ (BRM) +  ∠ (ARQ) )

            = 180 0  - ( 36 0  –  36 0 ) =  108 0

△  QEP cân tại E

⇒  ∠ (EQP) =  ∠ (EPQ) = ( 180 0 -  ∠ E )/2 = ( 180 0  -  108 0 )/2 =  36 0

∠ (AQR) + ∠ (RQP) +  ∠ (EQP) =  180 0

⇒  ∠ (RQP) =  180 0  - ( ∠ (AQR) +  ∠ (EQP) )

            =  180 0  - ( 36 0  –  36 0 ) =  108 0

∠ (EQP) +  ∠ (QPN) +  ∠ (DPN) =  180 0

⇒  ∠ (QPN) =  180 0  - ( ∠ (EPQ) +  ∠ (DPN) )

            =  180 0  - ( 36 0  –  36 0 ) =  108 0

Suy ra :  ∠ (PNM) =  ∠ (NMR) =  ∠ (MRQ) =  ∠ (RQP) =  ∠ (QPN)

Vậy MNPQR là ngũ giác đều.

Suy luận: Cung AB ngược hướng dương của đường tròn lượng giác nên có số đo âm, còn DA và EA có số đo dương. Do đó các phương án A, C, D bị loại.

Đáp án: B

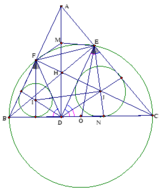
3) Chứng minh EM là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF

Tứ giác BFEC có  B E C ^ = B F C ^ = 90 0

=> tứ giác BFEC nội tiếp đường tròn đường kính BC

Gọi O là tâm đường tròn ngoại tiếp tứ giác BFEC thì O cũng là tâm đường tròn ngoại tiếp tam giác BEF

∆ OBE cân tại O (do OB=OE) => O B E ^ = O E B ^

∆ AEH vuông tại E có EM là trung tuyến ứng với cạnh huyền AH (Vì M là trung điểm AH)

=> ME=AH:2= MH do đó  ∆ MHE cân tại M=> M E H ^ = M H E ^ = B H D ^

Mà B H D ^ + O B E ^ = 90 0 ( ∆ HBD vuông tại D)

Nên  O E B ^ + M E H ^ = 90 0 Suy ra  M E O ^ = 90 0

⇒ E M ⊥ O E tại E thuộc ( O ) => EM là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF

4) Gọi I và J tương ứng là tâm đường tròn nội tiếp hai tam giác BDF và EDC. Chứng minh DIJ ^   =   DFC ^  

Tứ giác AFDC có A F C ^ = A D C ^ = 90 0  nên tứ giác AFDC nội tiếp đường tròn =>  B D F ^ = B A C ^

∆ BDF và  ∆ BAC có  B D F ^ = B A C ^  (cmt); B ^ chung do đó  ∆ BDF  ~   ∆ BAC(g-g)

Chứng minh tương tự ta có  ∆ DEC ~   ∆ ABC(g-g)

Do đó  ∆ DBF ~ ∆ DEC  ⇒ B D F ^ = E D C ^ ⇒ B D I ^ = I D F ^ = E D J ^ = J D C ^ ⇒ I D J ^ = F D C ^ (1)

Vì  ∆ DBF ~ ∆ DEC (cmt); DI là phân giác, DJ là phân giác  ⇒ D I D F = D J D C  (2)

Từ (1) và (2) suy ra  ∆ DIJ ~ ∆ DFC (c-g-c) =>  DIJ ^   =   DFC ^