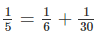Có bao nhiêu cách viết phân số \(\dfrac{1}{5}\) dưới dạng tổng của hai phân số \(\dfrac{1}{a}+\dfrac{1}{b}\) với \(0< a< b\) ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì 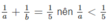 Suy ra a > 5 (1)
Suy ra a > 5 (1)
Ta lại có 0 < a < b nên 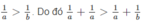
Hay 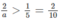 , suy ra a < 10 (2)
, suy ra a < 10 (2)
Từ (1) và (2) ta có a ∈ {6;7;8;9}
Nếu a = 6 thì 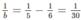 nên b = 30
nên b = 30
Nếu a = 7 thì 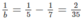 suy ra b = 17,5 (loại)
suy ra b = 17,5 (loại)
Nếu a = 8 thì 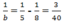 suy ra b ≈ 13,3 (loại)
suy ra b ≈ 13,3 (loại)
Nếu a = 9 thì 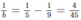 suy ra b = 11,25 (loại)
suy ra b = 11,25 (loại)
Vậy chỉ có một cách viết là 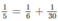

vì 1/a + 1/b = 1/5 nên 1/a < 1/5 => a >5 (1)
ta có: 0 < a < b nên 1/a > 1/b. do đó 1/a + 1/a > 1/a + 1/b
hay 2/a > 1/5 = 2/10
=> a < 10 (2)
từ (1) và (2) => a thuộc ( 6;7;8;9 )
nếu a = 6 thì 1/b = 1/5 - 1/6 = 1/30 nên b = 30
nếu a = 7 thì 1/b = 1/5 - 1/7 = 2/35 => b = 17,5 (loại)
nếu a = 8 thì 1/b = 1/5 - 1/8 = 3/40 => b = 13,3 (loại)
nếu a = 9 thì 1/b = 1/5 - 1/9 = 4/45 => b = 11,25 (loại)
vậy có 1 cách viết đó là 1/6 + 1/30 = 1/5
cái này mk vừa chữa sáng hôm qua trên lớp xong nên chắc chắn đúng đó k nha


a) \(\dfrac{2}{5}=\dfrac{1}{5}\cdot\dfrac{2}{1}\)
\(\dfrac{15}{12}=\dfrac{5}{4}=\dfrac{5}{2}\cdot\dfrac{1}{2}\)
\(\dfrac{5}{-12}=\dfrac{-5}{12}=\dfrac{-5}{3}\cdot\dfrac{1}{4}\)
\(\dfrac{-3}{-4}=\dfrac{3}{4}=\dfrac{3}{2}\cdot\dfrac{1}{2}\)

các ước của 5 là:
1.5 và 5.1
số 1 bằng tổng của các số:1+0
vậy ta có các cặp phân số:
(1/5+1/1)+(1/1+1/5)
vậy ta có 2 cách viết phân số

hực hiện phép nhân hoặc phép chia hai hỗn số bằng cách viết hỗn số dưới dạng phân số:
a) 512.334512.334 b) 613:429613:429
Giải
a) 512.334=112.154=1658;512.334=112.154=1658;
b) 6{1 \over 3}:4{2 \over 9} = {{19} \over 3}:{{38} \over 9} = {{19} \over 3}.{9 \over {38}} = {3 \over 2}\)
Lưu ý: Khi cộng hai hỗn số ta có thể cộng phần nguyên với nhau, phần phân số với nhau. Nhưng nhân (hoặc chia) hai hỗn số ta không thể nhân (hoặc chia) phần nguyên với nhau và phần phân số với nhau.
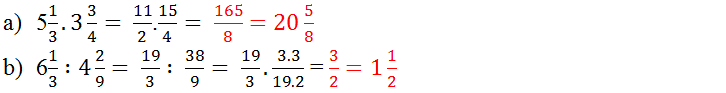
Giải:
Ta có:
Do \(\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{5}\Leftrightarrow\dfrac{1}{a}< \dfrac{1}{5}\Leftrightarrow a>5\left(1\right)\)
Ta lại có:
\(0< a< b\Leftrightarrow\dfrac{1}{a}>\dfrac{1}{b}\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{a}>\dfrac{1}{a}+\dfrac{1}{b}\)
Hay \(\dfrac{2}{a}>\dfrac{1}{5}\Leftrightarrow\dfrac{2}{a}>\dfrac{2}{10}\Leftrightarrow a< 10\left(2\right)\)
Kết hợp \(\left(1\right)\) và \(\left(2\right)\Leftrightarrow a\in\left\{6;7;8;9\right\}\)
- Với \(a=6\) thì \(\dfrac{1}{b}=\dfrac{1}{5}-\dfrac{1}{6}=\dfrac{1}{30}\Leftrightarrow b=30\)
- Với \(a=7\) thì \(\dfrac{1}{b}=\dfrac{1}{5}-\dfrac{1}{7}=\dfrac{2}{35}\Leftrightarrow b=17,5\) (loại)
- Với \(a=8\) thì \(\dfrac{1}{b}=\dfrac{1}{5}-\dfrac{1}{8}=\dfrac{3}{40}\Leftrightarrow b\approx13,3\) (loại)
- Với \(a=9\) thì \(\dfrac{1}{b}=\dfrac{1}{5}-\dfrac{1}{9}=\dfrac{4}{45}\Leftrightarrow b=11,25\) (loại)
Vậy chỉ có 1 cách viết là \(\dfrac{1}{5}=\dfrac{1}{6}+\dfrac{1}{30}\)
Vì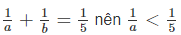 Suy ra a > 5 (1)
Suy ra a > 5 (1)
Ta lại có 0 < a < b nên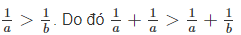
Hay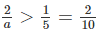 , suy ra a < 10 (2)
, suy ra a < 10 (2)
Từ (1) và (2) ta có a ∈ {6;7;8;9}
Nếu a = 6 thì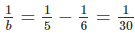 nên b = 30
nên b = 30
Nếu a = 7 thì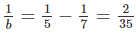 suy ra b = 17,5 (loại)
suy ra b = 17,5 (loại)
Nếu a = 8 thì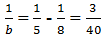 suy ra b ≈ 13,3 (loại)
suy ra b ≈ 13,3 (loại)
Nếu a = 9 thì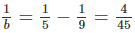 suy ra b = 11,25 (loại)
suy ra b = 11,25 (loại)
Vậy chỉ có một cách viết là