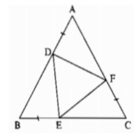
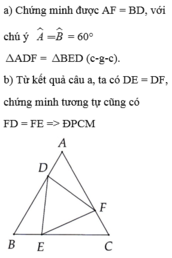
Cho tam giác đều ABC. Lấy các điểm D, E, F theo thứ tự thuộc các cạnh AB, BC, CA sao cho AD = BE = CF.
a) Chứng minh rằng tam giác DEF là tam giác đều có cùng tâm O với tam giác đều ABC
b) Chứng minh trung điểm I của EF chạy trên một đường cố định khi D , E , F chạy trên ba cạnh AB , BC , CA . Từ đó xác định vị trí của E , F để EF có độ dài nhỏ nhất ?
( các bạn giải hộ mình đi , mình đang cần gấp )