phân tích các đa thức sau thành nhân tử
Phân yichs các đa thức sau thành nhân tử
8) 4x^4-32x^2 + 1
9) 3(x4 + x2 + 1) - (x2 + x + 1)2
10) 64x4 + y4
11) a6 + a4 + a2b2 + b4 - b6
12) x3 + 3xy + y3 - 1
13) 4x4 + 4x3 + 5x2 + 2x + 1
14) x8 + x + 1
15) x8 + 3x4 + 4
16) 3x2 + 22xy + 11x + 37y + 7y2 +10
17) x4 - 8x + 63

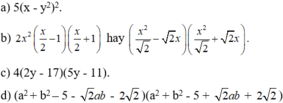
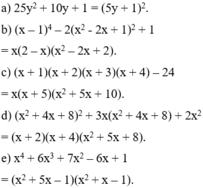
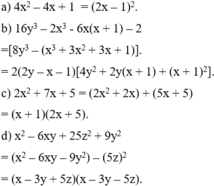
 k cho tui nha
k cho tui nha
9) \(3\left(x^4+x^2+1\right)-\left(x^2+x+1\right)^2\)
=\(3x^4+3x^2+3-\left(x^4+x^2+1+2x^3+2x+2x^2\right)\)
= \(3x^4+3x^2+3-x^4-x^2-1-2x^3-2x-2x^2\)
= \(2x^4-2x^3-2x+2\)
= \(2x^3.\left(x-1\right)-2.\left(x-1\right)\)
= \(\left(x-1\right)\left(2x^3-2\right)\)
= \(\left(x-1\right).2.\left(x^3-1\right)\)
= \(\left(x-1\right).2.\left(x-1\right)\left(x^2+x+1\right)\)
= \(\left(x-1\right)^2.2.\left(x^2+x+1\right)\)
10) \(64x^4+y^4\)
= \(\left(8x^2\right)^2+2.8x^2.y^2+\left(y^2\right)^2-16x^2y^2\)
= \(\left(8x^2+y^2\right)^2-\left(4xy\right)^2\)
= \(\left(8x^2+y^2-4xy\right).\left(8x^2+y^2+4xy\right)\)