1)so sánh
a)\(\dfrac{17}{15}\)và\(\dfrac{29}{37}\) b)\(\dfrac{12}{18}\)và\(\dfrac{13}{17}\) c)\(\dfrac{16}{51}\)và\(\dfrac{31}{90}\) d)\(\dfrac{2017}{2018}\)và\(\dfrac{2018}{2019}\) e)\(\dfrac{2018}{2017}\)và \(\dfrac{2019}{2018}\)
giúp mình nhé thank

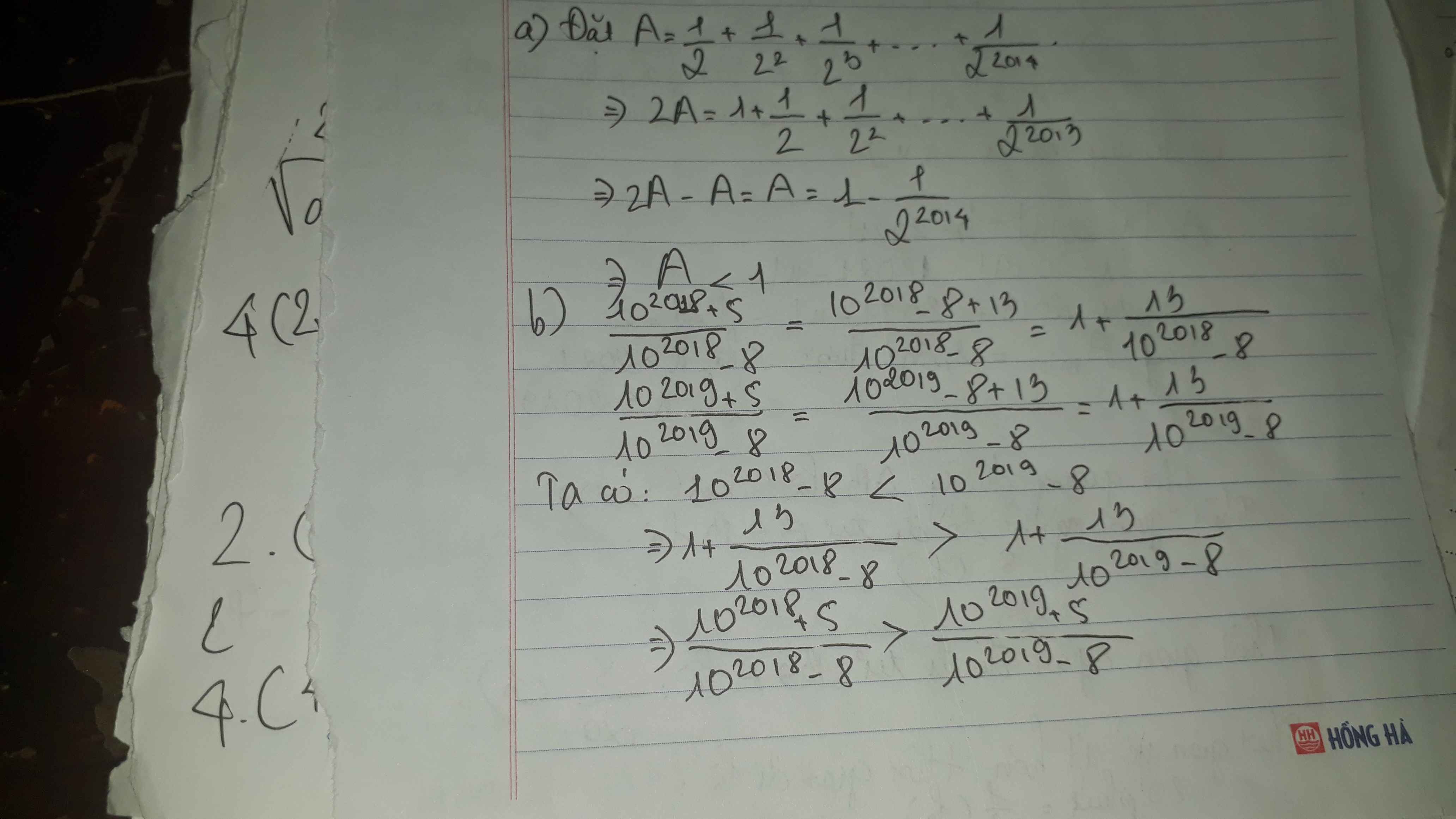
a)\(\dfrac{17}{15}>1;\dfrac{29}{37}< 1\Leftrightarrow\dfrac{17}{15}>\dfrac{29}{37}\)
b) \(\dfrac{13}{17}>\dfrac{13}{18}\Leftrightarrow\dfrac{13}{17}>\dfrac{12}{18}\)
d)\(1-\dfrac{2017}{2018}=\dfrac{1}{2018}\)
\(1-\dfrac{2018}{2019}=\dfrac{1}{2019}\)
\(\dfrac{1}{2018}>\dfrac{1}{2019}\Leftrightarrow\dfrac{2017}{2018}< \dfrac{2018}{2019}\)
e) \(\dfrac{2018}{2017}< 1;\dfrac{2019}{2018}>1\Leftrightarrow\dfrac{2018}{2017}< \dfrac{2019}{2018}\)