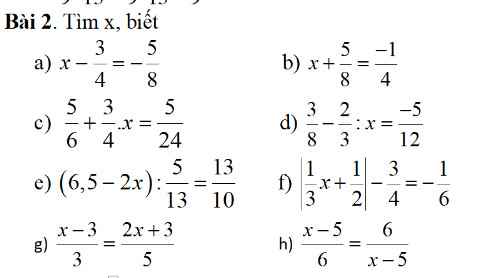
mn giúp mik nhanh lên nhé, mik sẽ tym cho mn :-D
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 4:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{5}=\dfrac{y}{6}=\dfrac{x+y}{5+6}=\dfrac{44}{11}=4\)
Do đó: x=20; y=24

h: Ta có: \(\dfrac{5}{x+3}=\dfrac{x+3}{5}\)
\(\Leftrightarrow\left(x+3\right)^2=25\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=-5\\x+3=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-8\\x=2\end{matrix}\right.\)


Bài 4:
a) Ta có: \(\widehat{yOz}+\widehat{xOy}=180^0\)(2 góc kề bù)
\(\Rightarrow\widehat{yOz}=180^0-\widehat{xOy}=180^0-50^0=130^0\)
b) Ta có: \(\widehat{zOt}=\widehat{yOt}=\dfrac{1}{2}\widehat{yOz}=\dfrac{1}{2}.130^0=65^0\)(do Ot là tia phân giác \(\widehat{yOz}\))
c) Ta có: \(\widehat{xOt}=\widehat{yOt}+\widehat{xOy}=65^0+50^0=115^0\)
Bài 5:
a) Ta có: \(\widehat{xOz}+\widehat{xOy}=180^0\)(2 góc kề bù)
\(\Rightarrow\widehat{xOz}=180^0-\widehat{xOy}=180^0-110^0=70^0\)
b) Ta có: \(\widehat{zOt}=\dfrac{1}{2}\widehat{xOz}=\dfrac{1}{2}.70^0=35^0\)( Ot là tia phân giác \(\widehat{xOz}\))
c) Ta có: \(\widehat{xOt}=\widehat{zOt}=35^0\)( Ot là tia phân giác \(\widehat{xOz}\))
Bài 4:
a: Ta có: \(\widehat{xOy}+\widehat{yOz}=180^0\)
\(\Leftrightarrow\widehat{yOz}=180^0-50^0\)
\(\Leftrightarrow\widehat{yOz}=130^0\)
b: \(\widehat{zOt}=\dfrac{\widehat{yOz}}{2}=65^0\)

=23 x (58-30) + 28 x 77
=23 x 28 +28 x 77
=28 x (23+77)
=28 x 100
=2800
học tốt bạn nhé
bài này là dạng nâng cao về toán tính nhanh, mik nghĩ là ẽ ít bạn trả lời đc

Bài 2:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y+z}{2+3+4}=\dfrac{9}{9}=1\)
Do đó: x=2; y=3; z=4
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{9}=\dfrac{x-3y+4z}{4-3\cdot3+4\cdot9}=\dfrac{62}{31}=2\)
Do đó: x=8; y=6; z=19
c: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+2y-3z}{2+2\cdot3-3\cdot4}=\dfrac{-20}{-4}=5\)
Do đó: x=10; y=15; z=20
Bài 1:
a: Ta có: \(\dfrac{x}{y}=\dfrac{9}{11}\)
nên \(\dfrac{x}{9}=\dfrac{y}{11}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{9}=\dfrac{y}{11}=\dfrac{x+y}{9+11}=\dfrac{60}{20}=3\)
Do đó: x=27; y=33
b: ta có: \(\dfrac{x}{y}=\dfrac{1.2}{2.5}\)
nên \(\dfrac{x}{12}=\dfrac{y}{25}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{12}=\dfrac{y}{25}=\dfrac{y-x}{25-12}=\dfrac{26}{13}=2\)
Do đó: x=24; y=50
c: Ta có: \(7x=4y\)
nên \(\dfrac{x}{4}=\dfrac{y}{7}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{7}=\dfrac{y-x}{7-4}=\dfrac{33}{3}=11\)
Do đó: x=44; y=77
d:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{-7}=\dfrac{y}{4}=\dfrac{2x-3y}{-14-12}=\dfrac{-78}{-26}=3\)
Do đó: x=-21; y=12

15×2121/4343+15×222222/434343
= 15 x (21x101)/(101x43) + 15x(22x 10101)/(43x10101)
= 15 x 21/43 + 15 x 22/43
= 15x(21/43 + 22/43)
= 15x1 = 15

Bài 1:
c: Đặt \(\dfrac{x}{3}=\dfrac{y}{4}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=3k\\y=4k\end{matrix}\right.\)
Ta có: xy=48
\(\Leftrightarrow12k^2=48\)
\(\Leftrightarrow k^2=4\)
Trường hợp 1: k=2
\(\Leftrightarrow\left\{{}\begin{matrix}y=3k=3\cdot2=6\\y=4k=4\cdot2=8\end{matrix}\right.\)
Trường hợp 2: k=-2
\(\Leftrightarrow\left\{{}\begin{matrix}y=3k=3\cdot\left(-2\right)=-6\\y=4k=4\cdot\left(-2\right)=-8\end{matrix}\right.\)
a) \(x-\dfrac{3}{4}=-\dfrac{5}{8}\Rightarrow x=-\dfrac{5}{8}+\dfrac{3}{4}\Rightarrow x=\dfrac{1}{8}\)
b) \(x+\dfrac{5}{8}=-\dfrac{1}{4}\Rightarrow x=-\dfrac{1}{4}-\dfrac{5}{8}\Rightarrow x=-\dfrac{7}{8}\)
c) \(\dfrac{5}{6}+\dfrac{3}{4}x=\dfrac{5}{24}\Rightarrow x=\left(\dfrac{5}{24}-\dfrac{5}{6}\right):\dfrac{3}{4}\Rightarrow x=-\dfrac{5}{6}\)
d) \(\dfrac{3}{8}-\dfrac{2}{3}:x=-\dfrac{5}{12}\Rightarrow\dfrac{2}{3}:x=\dfrac{3}{8}+\dfrac{5}{12}\Rightarrow\dfrac{2}{3}:x=\dfrac{19}{24}\Rightarrow x=\dfrac{2}{3}:\dfrac{19}{24}=\dfrac{16}{19}\)
a) \(x-\dfrac{3}{4}=-\dfrac{5}{8}\\ \Rightarrow x=\dfrac{1}{8}\)
b) \(x+\dfrac{5}{8}=-\dfrac{1}{4}\\ \Rightarrow x=-\dfrac{7}{8}\)
c) \(\dfrac{5}{6}+\dfrac{3}{4}x=\dfrac{5}{24}\\ \Rightarrow\dfrac{3}{4}x=-\dfrac{5}{8}\\ \Rightarrow x=-\dfrac{5}{6}\)
d) \(\dfrac{3}{8}-\dfrac{2}{3}:x=-\dfrac{5}{12}\\ \Rightarrow\dfrac{2}{3}:x=\dfrac{19}{24}\\ \Rightarrow x=\dfrac{16}{19}\)
e) \(\left(6,5-2x\right):\dfrac{5}{13}=\dfrac{13}{10}\\ \Rightarrow6,5-2x=\dfrac{1}{2}\\ \Rightarrow2x=6\\ \Rightarrow x=3\)
f) \(\left|\dfrac{1}{3}x+\dfrac{1}{2}\right|-\dfrac{3}{4}=-\dfrac{1}{6}\\ \Rightarrow\left|\dfrac{1}{3}x+\dfrac{1}{2}\right|=\dfrac{7}{12}\\ \Rightarrow\left[{}\begin{matrix}\dfrac{1}{3}x+\dfrac{1}{2}=\dfrac{7}{12}\\\dfrac{1}{3}x+\dfrac{1}{2}=-\dfrac{7}{12}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}\\x=-\dfrac{13}{4}\end{matrix}\right.\)
g) \(\dfrac{x-3}{3}=\dfrac{2x+3}{5}\\ \Rightarrow5x-15=6x+9\\ \Rightarrow-x=24\\ \Rightarrow x=-24\)
h) \(\dfrac{x-5}{6}=\dfrac{6}{x-5}\\ \Rightarrow\left(x-5\right)^2=6^2\\ \Rightarrow\left[{}\begin{matrix}x-5=-6\\x-5=6\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-1\\x=11\end{matrix}\right.\)