a) Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:

\(AB^2=AH^2+HC^2\)

\(\Leftrightarrow AH^2=15^2-9^2=144\)

hay AH=12(cm)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(AH^2=HB\cdot HC\)

\(\Leftrightarrow HC=\dfrac{12^2}{9}=16\left(cm\right)\)

a. Trọng lượng của vật là:

P=10.m= 10.15=150N

Trọng lực có phương thẳng đứng, chiều từ trên xuống dưới.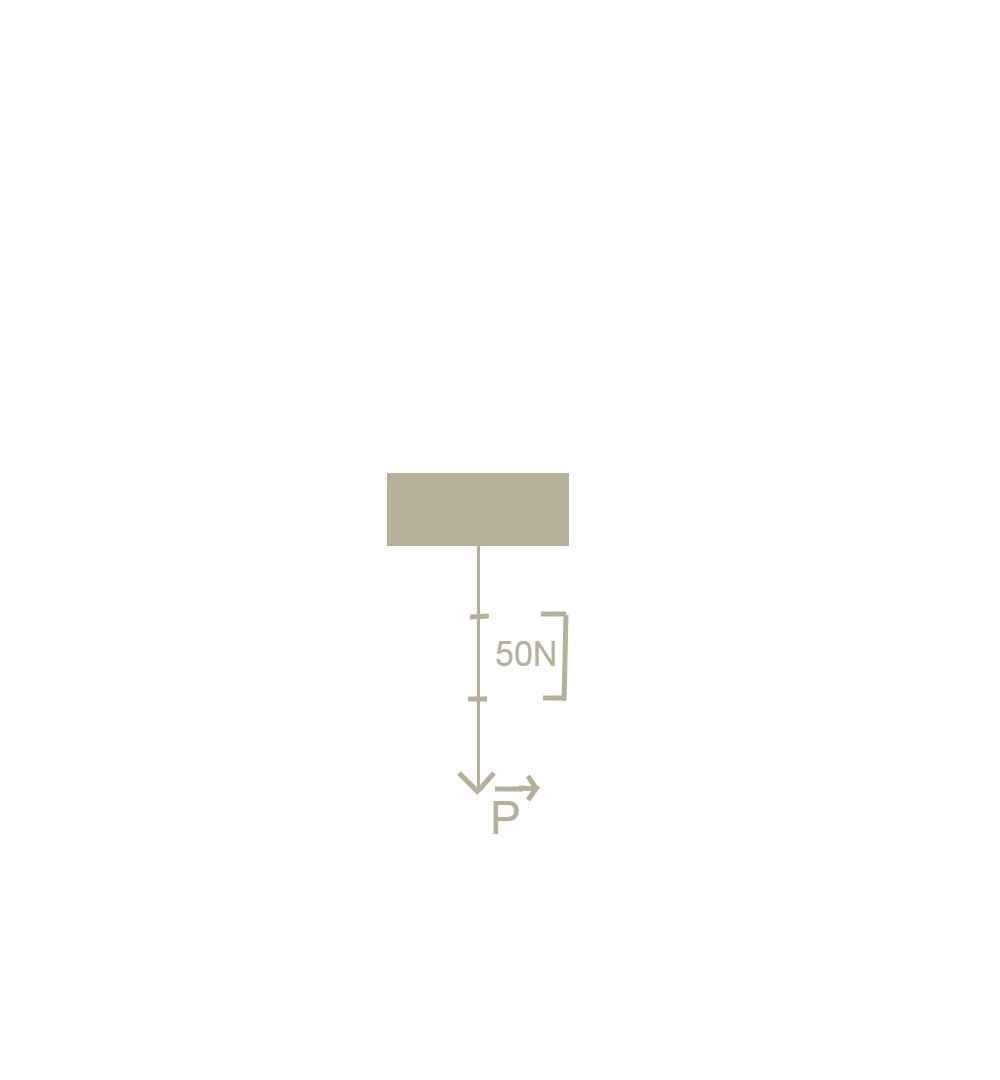b. 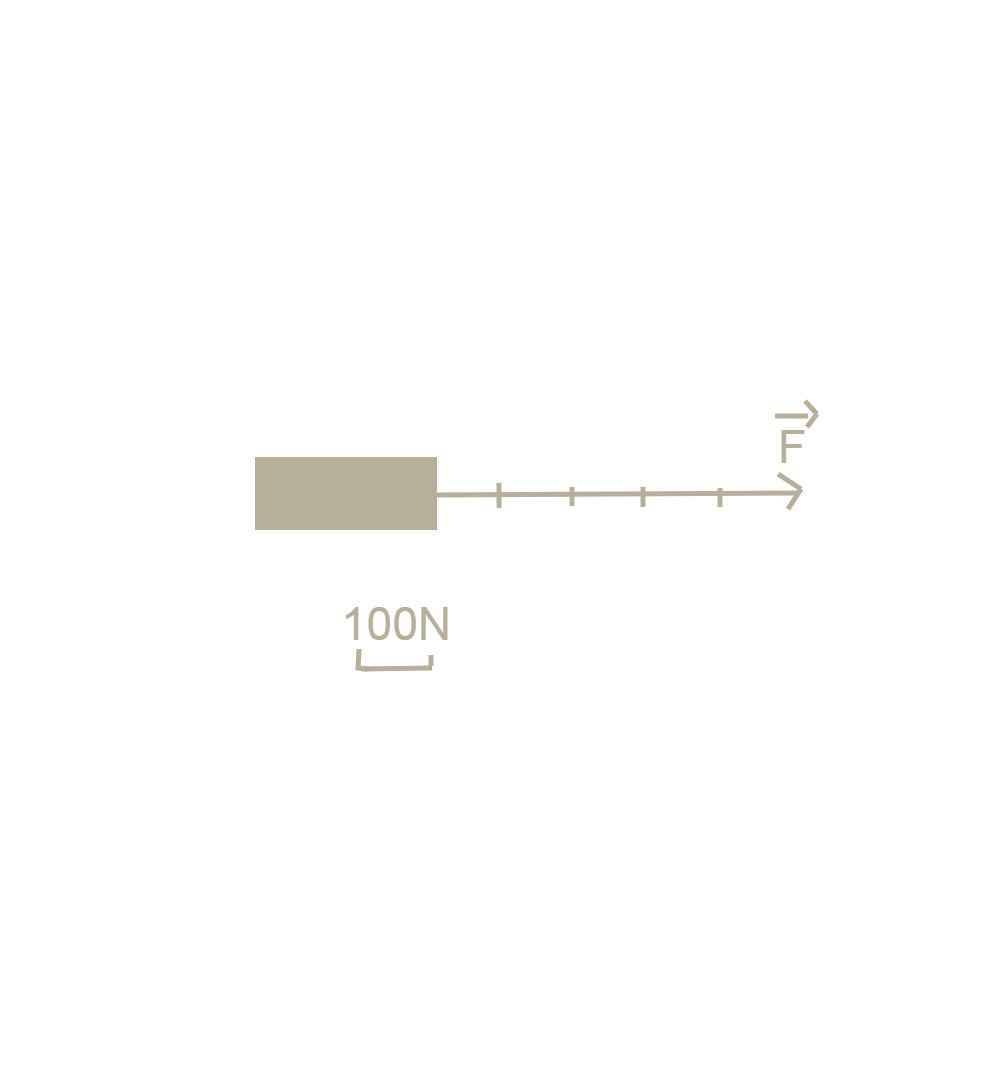c.Trọng lượng của vật là:

P= 10.m= 10.6=60N

Trọng lượng có phương thẳng, đứng chiều từ trên xuống dưới.

Vì vật đang đứng yên, nên chứng tỏ đã có 2 lực cân bằng tác dụng vào vật. Đó là trọng lực và lực nâng (P = Q)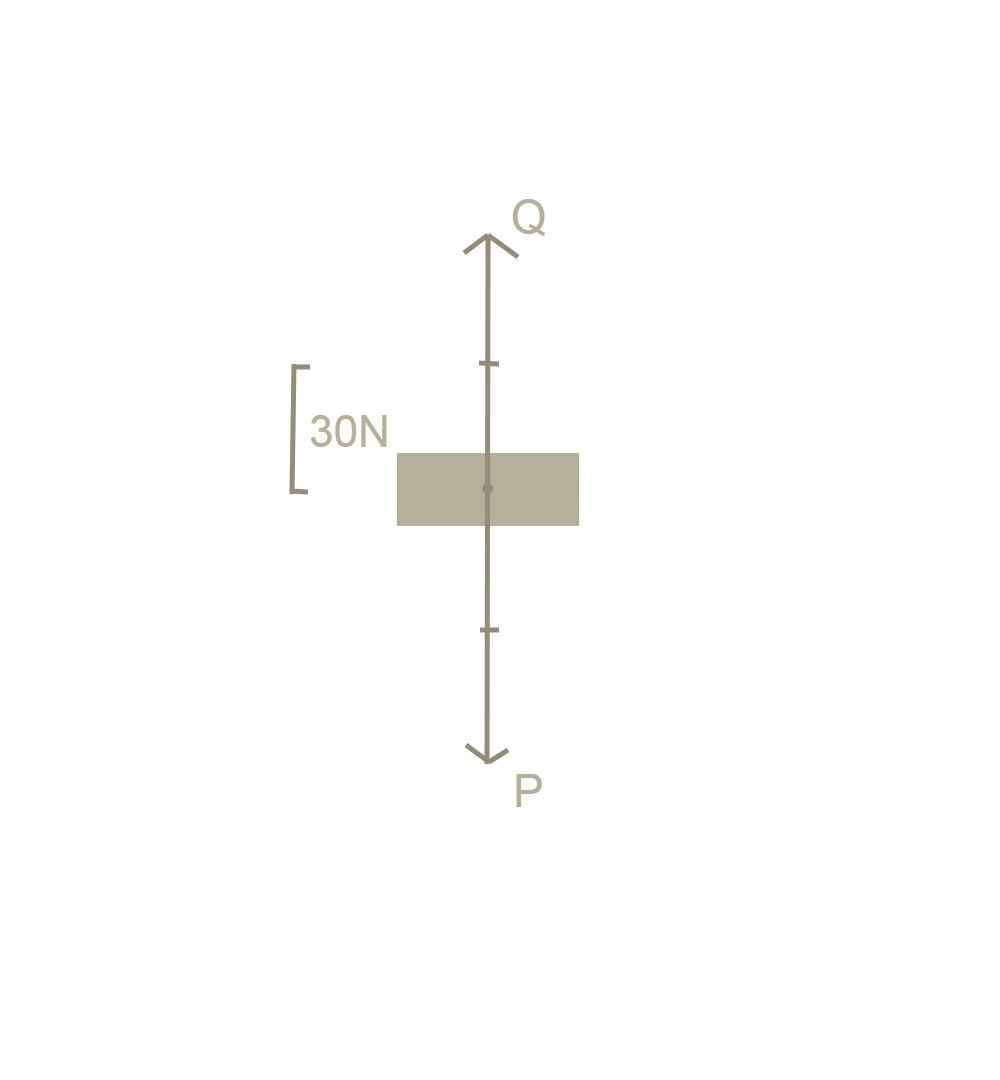

Bài 4 Xét \(\Delta ABC\) vuông tại B

\(\widehat{BAC}+\widehat{ACB}=90^o\\ \Rightarrow\widehat{ACB}=90^o-30^o=60^o\)

Theo định lý sin

\(\dfrac{AB}{sinC}=\dfrac{BC}{sinA}\\ \Rightarrow BC=\dfrac{AB.sinA}{sinC}=\dfrac{2.sin30^o}{sin60^o}=\dfrac{2\sqrt{3}}{3}\)

Theo định lý Pytago :

\(AB^2+BC^2=AC^2\\ \Rightarrow AC=\sqrt{AB^2+BC^2}=\sqrt{2^2+\left(\dfrac{2\sqrt{3}}{3}\right)^2}=\dfrac{4\sqrt{3}}{3}\)

Bài 5

Chiều dài mặt phẳng nghiêng là : 

\(5:sin36^o=8,5\left(m\right)\)

4:

góc BCA=90-30=60 độ

cos BAC=BA/CA

=>2/CA=cos30=căn 3/2

=>CA=4/căn 3(cm)

=>CB=1/2*4/căn 3=2/căn 3(cm)

Bài 5;

Gọi mp nghiêng là AB, chiều cao là AC

=>ΔACB vuông tại C có AC=5m và góc B=36 độ

ΔABC vuông tại C nên sin ABC=AC/AB

=>5/AB=sin36

=>AB=8,51(m)

\(36,\dfrac{6+2\sqrt{6}}{\sqrt{3}+\sqrt{2}}=\dfrac{\left(6+2\sqrt{6}\right)\left(\sqrt{3}-\sqrt{2}\right)}{\left(\sqrt{3}+\sqrt{2}\right)\left(\sqrt{3}-\sqrt{2}\right)}=\dfrac{6\sqrt{3}-6\sqrt{2}+6\sqrt{2}-4\sqrt{3}}{\sqrt{3^2}-\sqrt{2^2}}=\dfrac{2\sqrt{3}}{3-2}=2\sqrt{3}\)

\(35,\dfrac{5\sqrt{6}+6\sqrt{5}}{\sqrt{5}+\sqrt{6}}=\dfrac{\sqrt{6}.\sqrt{5}\left(\sqrt{5}+\sqrt{6}\right)}{\sqrt{5}+\sqrt{6}}=\sqrt{30}\)

\(34,\dfrac{6\sqrt{2}-4}{\sqrt{2}-3}\\ =\dfrac{\left(6\sqrt{2}-4\right)\left(\sqrt{2}+3\right)}{\left(\sqrt{2}-3\right)\left(\sqrt{2}+3\right)}\\ =\dfrac{6.2+3.6\sqrt{2}-4\sqrt{2}-12}{\sqrt{2^2}-3^2}\\ =\dfrac{12+18\sqrt{2}-4\sqrt{2}-12}{2-9}\\ =-2\sqrt{2}\)

\(33,\dfrac{3\sqrt{2}-2\sqrt{3}}{\sqrt{3}-\sqrt{2}}=\dfrac{\sqrt{3}.\sqrt{2}\left(\sqrt{3}-\sqrt{2}\right)}{\sqrt{3}-\sqrt{2}}=\sqrt{6}\)

Bài V:

-ĐKXĐ: \(x\ne\pm1\).

\(\dfrac{m}{x-1}+\dfrac{x}{x+1}=\dfrac{x^2}{x^2-1}\)

\(\Leftrightarrow\dfrac{m\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{x\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}\)

\(\Rightarrow mx+m+x^2-x=x^2\)

\(\Leftrightarrow m\left(x+1\right)=x\)

\(\Leftrightarrow m=\dfrac{x}{x+1}\)

-Vì m,x nguyên:

\(\Rightarrow x⋮\left(x+1\right)\)

\(\Rightarrow\left(x+1-1\right)⋮\left(x+1\right)\)

\(\Rightarrow-1⋮\left(x+1\right)\)

\(\Rightarrow\left(x+1\right)\in\left\{1;-1\right\}\)

\(\Rightarrow x\in\left\{0;-2\right\}\) (nhận)

*\(x=0\Rightarrow m=\dfrac{x}{x+1}=\dfrac{0}{0+1}=0\)

\(x=-2\Rightarrow m=\dfrac{x}{x+1}=\dfrac{-2}{-2+1}=1\)

-Vậy với \(m=0\) thì \(S=\left\{0\right\}\)

         với \(m=1\) thì \(S=\left\{-2\right\}\)

3. She said I should ask a lawyer.

4. Mrs Linh asked me to give Tuan this book.

Câu 3: 

a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)

b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)

nên BC<AC=AB

c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có

BC chung

\(\widehat{EBC}=\widehat{DCB}\)

Do đó:ΔEBC=ΔDCB

d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)

nên ΔOBC cân tại O

Câu 2

a) Thay y = -2 vào biểu thức đã cho ta được:

2.(-2) + 3 = -1

Vậy giá trị của biểu thức đã cho tại y = -2 là -1

b) Thay x = -5 vào biểu thức đã cho ta được:

2.[(-5)² - 5] = 2.(25 - 5) = 2.20 = 40

Vậy giá trị của biểu thức đã cho tại x = -5 là 40

Đăng lại vì ko ai giải 🥺

thôi bọn mềnh cũng chệu boạn nhóe

\(\left|2x-3\right|=3-2x\)

\(ĐK:x\le\dfrac{3}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)

Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)

ok nha

A = 1/2 + 1/6 + 1/16 + ... + 1/4084441   có : 2021 - 1 + 1 = 2021 số

1 = 1/2021 + 1/2021 + ... + 1/2021   có 2021 số 

vậy 1 > A