Giải chi tiết hộ em câu 2 ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số sản phẩm dự định là a (sản phẩm ) (a là số tự nhiên khác 0)
Vì theo dự định mỗi ngày sản xuất 50 sản phẩm nên số ngày theo dự định là \(\dfrac{a}{50}\)
Nhưng thực tế , đội đã sản xuất theeo được 30 sản phẩm do mỗi ngày vượt mức 10 sản phẩm (nghĩa là sản xuất 60 sản phẩm) , nên số ngày thực tế là \(\dfrac{a+30}{60}\)
Vì thực tế sớm hơn dự định 2 ngày nên ta có phương trình :
\(\dfrac{a}{50}=\dfrac{a+30}{60}+2\\ \Leftrightarrow6a=5\left(a+30+120\right)\\\Leftrightarrow a=750\left(t.m\right) \)
Vậy số sản phẩm dự định là 750 sản phẩm
Bài 3:
Gọi số sản phẩm đội phải sản xuất theo kế hoạch là x( sản phẩm, x\(\in N\)*)
Thời gian đội sản xuất theo kế hoạch là: \(\dfrac{x}{50}\) (ngày)
Số ngày làm thực tế là: \(\dfrac{x+30}{50+10}=\dfrac{x+30}{60}\) (ngày)
Theo bài ra, ta có phương trình:
\(\dfrac{x}{50}-\dfrac{x+30}{60}=2\)
\(\Leftrightarrow\dfrac{60x-50\left(x+30\right)}{50.60}=2\)
\(\Leftrightarrow60x-50x-1500=6000\Leftrightarrow x=750\)(thoả mãn)
Vậy theo kế hoạch đội phải sản xuất 750 sản phẩm

\(b,B=\dfrac{x-4+2\sqrt{x}+6-3\sqrt{x}-4}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ B=\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\\ c,M=B:A=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{x-\sqrt{x}+2}=\dfrac{\sqrt{x}+1}{x-\sqrt{x}+2}\\ M=\dfrac{x-\sqrt{x}+2-x+2\sqrt{x}-1}{x-\sqrt{x}+2}\\ M=1-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}+2}=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\)
Ta có \(\left(\sqrt{x}-1\right)^2\ge0;x-\sqrt{x}+2=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
Do đó \(\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\ge0\)
\(\Leftrightarrow M=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\le1-0=1\)
Vậy \(M_{max}=1\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(tm\right)\)
a: Thay \(x=3+2\sqrt{2}\) vào A, ta được:
\(A=\dfrac{3+2\sqrt{2}-\sqrt{2}-1+2}{\sqrt{2}+1+3}=\dfrac{4+\sqrt{2}}{4+\sqrt{2}}=1\)

Có : G - T = 140 nu
2T + 3G = 2520
=> A = T = 420 nu
G = X = 560 nu
N = 2 ( A + G ) = 1960 nu
l = N x 3,4 : 2 = 3332Ao
Ta có: \(G-T=140\)
\(2T+3G=2520\)
\(\Rightarrow\left\{{}\begin{matrix}A=T=420nu\\G=X=560nu\end{matrix}\right.\)
\(N=2A+2G=2\cdot420+2\cdot560=1960nu\)
\(l=\dfrac{2N}{3,4}=\dfrac{2\cdot1960}{3,4}=1152,94A^o\)

Câu 1 em mở SGK nha
Câu 2:
a) Fe2O3 + 3 H2 -to-> 2 Fe + 3 H2O
b) HgO + H2 -to->Hg + H2O
c)PbO + H2 -to-> Pb + H2O
Câu 3:
nHgO= 21,7/217=0,1(mol)
PTHH: HgO + H2 -to-> Hg + H2O
0,1________0,1_______0,1(mol)
a) nHg= 0,1.201=20,1(g)
b)mH2=0,1.2=0,2(g)
V(H2,đktc)=0,1.22,4=2,24(l)
4)
nH2= 8,4/22,4=0,375(mol)
PTHH: H2 + 1/2 O2 -to-> H2O
0,375__________________0,375
=>mH2O=0,375.18= 6,75(g)

a: Xét ΔABD và ΔACD có
AB=AC
BD=CD
AD chung
Do đó: ΔABD=ΔACD
b: ΔABD=ΔACD
=>\(\widehat{ADB}=\widehat{ADC}\)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
c: Ta có: \(\widehat{ADB}=90^0\)
=>AD\(\perp\)BC tại D
D là trung điểm của BC
=>\(DB=DC=\dfrac{BC}{2}=\dfrac{24}{2}=12\left(cm\right)\)
ΔADB vuông tại D
=>\(AD^2+DB^2=AB^2\)
=>\(AD^2=20^2-12^2=256\)
=>\(AD=\sqrt{256}=16\left(cm\right)\)
Xét ΔABC có
AD là đường trung tuyến
G là trọng tâm
Do đó: \(AG=\dfrac{2}{3}AD=\dfrac{2}{3}\cdot16=\dfrac{32}{3}\left(cm\right)\)


Gửi muộn thế em, giờ này ít người thức khuya lắm
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\)
\(\left\{{}\begin{matrix}Ox:F-F_{ms}-mg\sin\alpha=m.a\\Oy:N=mg\cos\alpha\end{matrix}\right.\)
\(\Rightarrow F-\mu mg\cos\alpha-mg\sin\alpha=m.a\Rightarrow F=...\)

ĐKXĐ: \(-1\le x\le4\)
\(\Leftrightarrow\left(x-3\right)\sqrt{1+x}-\left(x-3\right)+x-x\sqrt{4-x}=2x^2-6x\)
\(\Leftrightarrow\left(x-3\right)\left(\sqrt{1+x}-1\right)+x\left(1-\sqrt{4-x}\right)=2x^2-6x\)
\(\Leftrightarrow\dfrac{x\left(x-3\right)}{\sqrt{1+x}+1}+\dfrac{x\left(x-3\right)}{1+\sqrt{4-x}}=2\left(x^2-3x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-3x=0\Rightarrow x=...\\\dfrac{1}{\sqrt{1+x}+1}+\dfrac{1}{1+\sqrt{4-x}}=2\left(1\right)\end{matrix}\right.\)
Xét (1), do \(VT< \dfrac{1}{1}+\dfrac{1}{1}=2\Rightarrow VT< VP\Rightarrow\left(1\right)\) vô nghiệm
Vậy ...






 giải chi tiết hộ em ạ
giải chi tiết hộ em ạ 
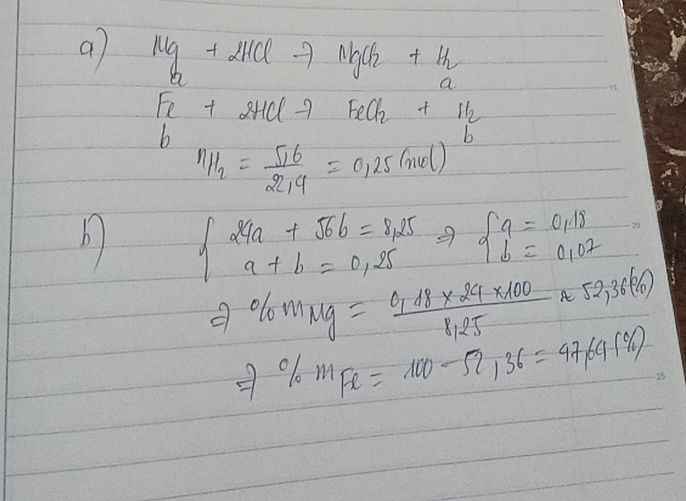
 Giải chi tiết hộ em với ạ
Giải chi tiết hộ em với ạ