giả xử z = a/m , y=b/m
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


do x<y =>a/m<b/m=>a<b
ta có:
x=a/m=2a/2m
y=b/m=2b/2m
do a<b=>a+a/2m<a+b/2m
<=>2a/2m<a+b/2m
<=>x<z (1)
do a<b=>a+b/2m<b+b/2m
<=>a+b/2m<2b/2m
<=>z<y (2)
từ (1) và (2)=>ĐPCM

x =a/m =>. x = 2a/2m
y =b/m => y = 2b/2m
z = (a+b)/2m
theo giả thiết a < b => a + b < b + b => a + b < 2b ........(1)
Ngòa i ra, a < b => a + a < a + b => 2a < a + b ........(2)
Suy ra:
2a < a +b < 2b
Suy ra (chia 2 vế cho 2m) :
2a/2m < (a +b)/2m < 2b
R út gọn ta được : x < z <y

Ta có:
x = \(\frac{a}{m}\)\(\Rightarrow\)x = \(\frac{2a}{2m}\Rightarrow\)x = \(\frac{a+a}{2m}\)
y = \(\frac{b}{m}\Rightarrow\)y = \(\frac{2b}{2m}\Rightarrow\)y = \(\frac{b+b}{2m}\)
Mà x < y \(\Rightarrow\) a < b \(\Rightarrow\)a + a < b + b
Vì a + a < b + b \(\Rightarrow\)\(\frac{a+a}{2m}\) < \(\frac{a+b}{2m}\) < \(\frac{b+b}{2m}\Rightarrow\)\(\frac{a}{m}\)< \(\frac{a+b}{m}\) < \(\frac{b}{m}\)
Vậy x < z < y


C1:
Ta có: \(x=\frac{a}{m}=\frac{2a}{2m}\) và \(y=\frac{b}{m}=\frac{2b}{2m}\)
Vì x<y nên a<b
Vì 2a< a+b< 2b
=> \(\frac{2a}{2m}

m>0 và x<y nên a<b Do đó \(x=\frac{a}{m}=\frac{2a}{2m}=\frac{a+a}{2m}


Vì x < y nên 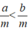 mà m > 0 nên a < b. Ta có
mà m > 0 nên a < b. Ta có
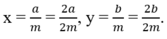
Chọn số 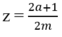 . Do 2a < 2a + 1 và m > 0 nên
. Do 2a < 2a + 1 và m > 0 nên 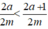 hay x < z. (1)
hay x < z. (1)
Do a < b và a; b ∈ Z nên a + 1 ≤ b suy ra 2a + 2 ≤ 2b.
Ta có 2a + 1 < 2a + 2 ≤ 2b nên 2a + 1 < 2b, do đó 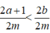 hay z < y. (2)
hay z < y. (2)
Từ (1) và (2) suy ra: x < z < y