Bài 1: Hàm số f(x) có đạo hàm trên R và f'(x) > 0 \(\forall\) x \(\in\) (0; +\(\infty\)), biết f(1)=2. Khẳng định nào sau đây có thể xảy ra ?
A.f(2)=1 B. f(2)+f(3)=4
C. f(2016)>f(2017) D. f(-1)=4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có Đáp án D
Ta có y’ = –f’(1 – x) + 2018 = –[1–(1–x)][(1–x)+2]g(1–x) – 2018 + 2018
= –x(3–x)g(1–x)
Suy ra 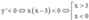 (vì g(1–x) < 0,
∀
x
∈
R
)
(vì g(1–x) < 0,
∀
x
∈
R
)
Vậy hàm số đã cho nghịch biến trên khoảng 3 ; + ∞
ý D có thể xảy ra vì gt chỉ cho h/s đồng biến trên (0;+\(\infty\))