Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo. Gọi M, N thứ tự là trung điểm của OD và OB. Gọi E là giao điểm của AM và CD. F là giao của CN và AB.
a) CM tứ giác AMCN là hình bình hành.
b) Tứ giác AECF là hình gì? Chứng minh.
c) CM E và F đối xứng với nhau qua O.
d) Chứng minh EC=2DE

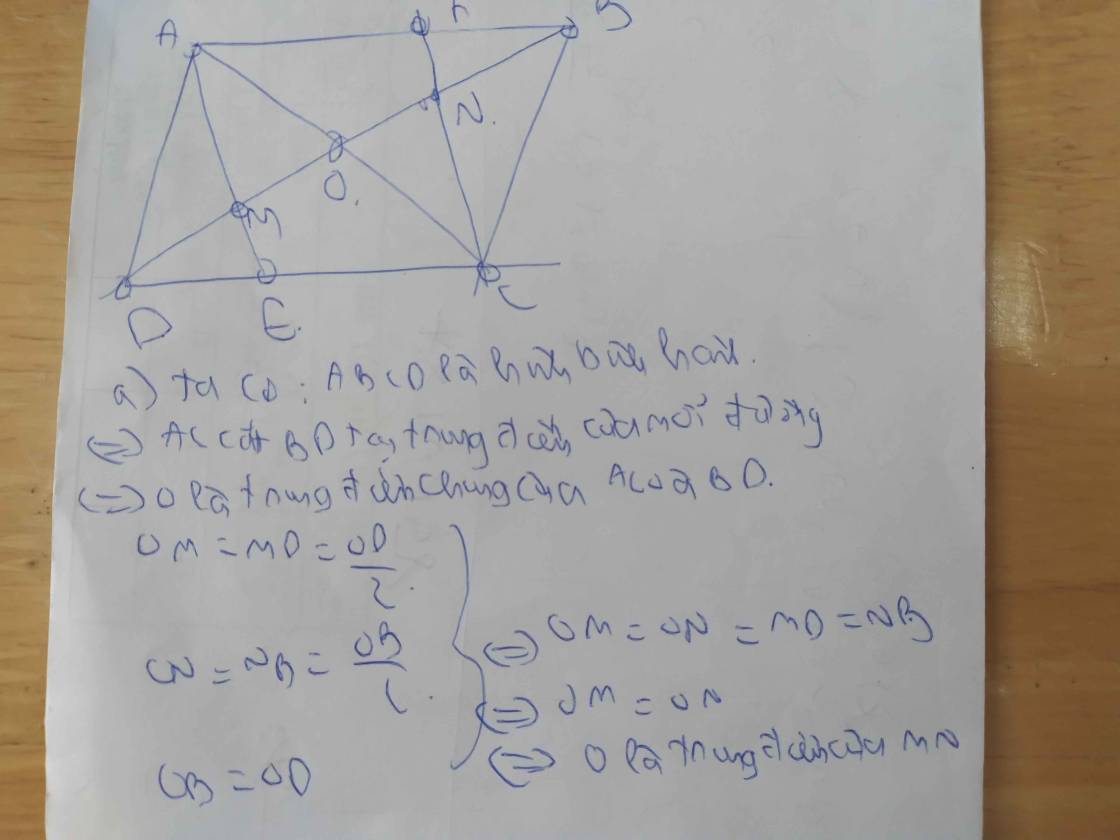


a) Ta có OM=1/2OD
ON=1/2OB
Mà OD=OB
=>OM=ON
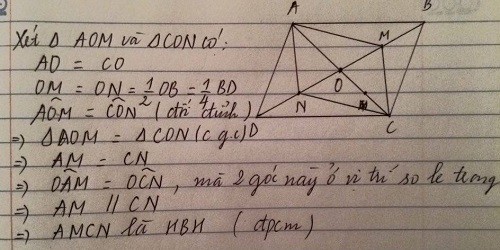
Xét tứ giác AMCN có OA=OC(gt),OM=ON(cmt)
=>AMCN là hình bình hành
b)Ta có AB//DC(gt) hay AF//CE(1)
AM//CN(AMCN là hình bình hành) hay AE//CF(2)
Từ (1) và (2)=>AECF là hình bình hành.
c)Ta có AECF là hình bình hành
Mà OA=OC(gt)
=>O là giao điểm hai đường chéo
=>O là trung điểm của EF
=>OE=OF
=>E và F đối xứng với nhau qua O