Cho tam giác ABC , trọng tâm G.
a) Vẽ đường thẳng d qua G,cắt các đoạn thẳng AB,AC . Gọi A',B',C' là hình chiếu của của A,B,C trên d.Tìm liên hệ giữa các độ dài AA',BB',CC'có liên hệ gì?
b) Nếu ngoài đường thẳng d nằm ngoài tam giác ABC và G' là hình chiếu của G trên d thì các độ dài GG',AA',BB',CC' có liên hệ gì?
Help me!!!!!!!!!!!!!


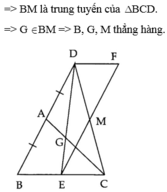
Gọi D là trung điểm BC, E là trung điểm AG. D' và E' lần lượt là hình chiếu của D và E trên đường thẳng d.
Vì G là trọng tậm tam giac ABC, D là trung điểm BC, E là trug điểm AG, suy ra AE=EG=GD.
Xét tứ giác DD'E'E, ta có : GD=GE vad GG'//EE'//DD'( cùng vuông góc với đường thẳng d ), suy ra GG' là đường trung bình của hình thang DD'E'E, suy ra 2GG'=EE'+DD'.
Chứng minh tương tự với tứ giác BB'C'C và tứ giác AA'G'G, ta được D là đường trung bình của tứ giác BB'C'C suy ra 2DD;=BB' + CC (1)',
EE' là đường trung bình của hình thang AA'G;G suy ra 2EE'=AA'+GG (2)'.
Ta có EE'+ DD' = 2 GG' ( * ) <=> 2EE' + 2DD' = 4GG'. Thay (1) và (2) vào (*) ta đc : AA' + GG' +BB' + CC' = 4GG' <=> AA' + BB' + CC' = 3GG'